Introduction to statistical data analysis
August 27, 2011 at 01:55 PM | categories: data analysis | View Comments
Contents
Introduction to statistical data analysis
clear all
clc
Problem statement.
Given several measurements of a single quantity, determine the average value of the measurements, the standard deviation of the measurements and the 95% confidence interval for the average.
the data
y = [8.1 8.0 8.1];
the average and standard deviation
ybar = mean(y) s = std(y)
ybar =
8.0667
s =
0.0577
the confidence interval
This is a recipe for computing the confidence interval. The strategy is:
- compute the average
- Compute the standard deviation of your data
- Define the confidence interval, e.g. 95% = 0.95
- compute the student-t multiplier. This is a function of the confidence interval you specify, and the number of data points you have minus 1. You subtract 1 because one degree of freedom is lost from calculating the average.
The confidence interval is defined as ybar +- T_multiplier*std/sqrt(n).
the tinv command provides the T_multiplier
ci = 0.95; alpha = 1 - ci; n = length(y); %number of elements in the data vector T_multiplier = tinv(1-alpha/2, n-1) % the multiplier is large here because there is so little data. That means % we do not have a lot of confidence on the true average or standard % deviation ci95 = T_multiplier*s/sqrt(n) % confidence interval sprintf('The confidence interval is %1.1f +- %1.1f',ybar,ci95) [ybar - ci95, ybar + ci95] % we can say with 95% confidence that the true mean lies between these two % values. % categories: Data analysis
T_multiplier =
4.3027
ci95 =
0.1434
ans =
The confidence interval is 8.1 +- 0.1
ans =
7.9232 8.2101
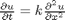
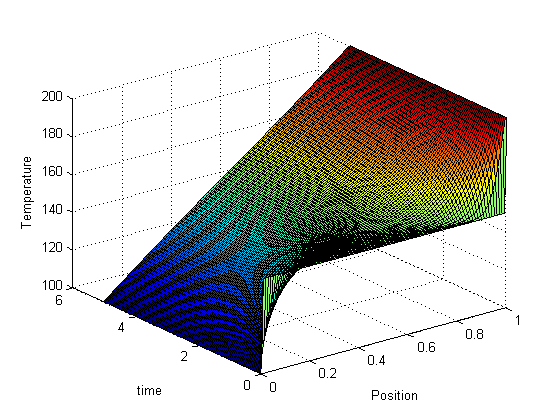
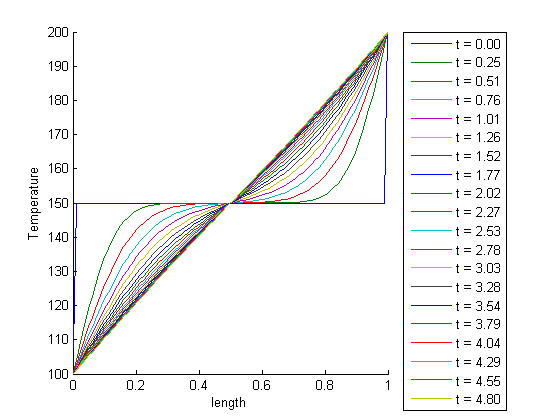
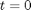 , in this example we have
, in this example we have 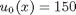 as an initial condition. with boundary conditions
as an initial condition. with boundary conditions 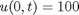 and
and 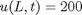 .
.
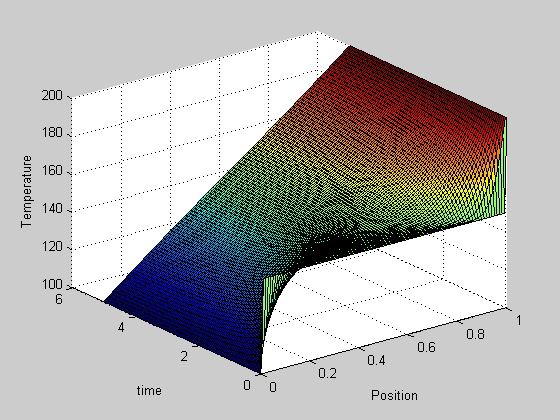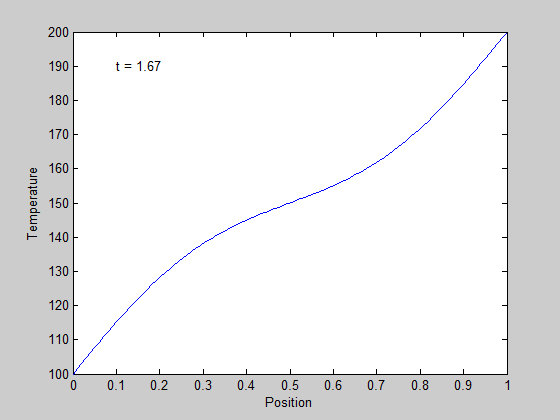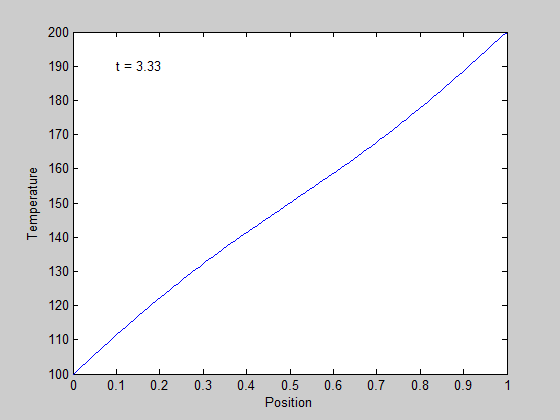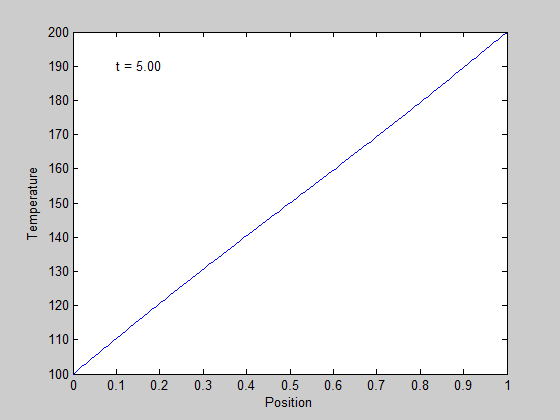
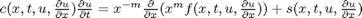
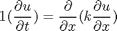
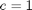 ,
,  , and
, and 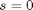
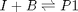
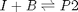
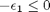
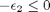
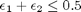
![$A = \left[ \begin{array}{cc} -1 & 0 \\ 0 & -1 \\ 1 & 1 \end{array} \right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/08/Gmin_eq10921.png) and
and ![$b = \left[ \begin{array}{c} 0 \\ 0 \\ 0.5\end{array} \right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/08/Gmin_eq62028.png)