transient heat conduction - partial differential equations

adapated from http://msemac.redwoods.edu/~darnold/math55/DEproj/sp02/AbeRichards/slideshowdefinal.pdf

Contents

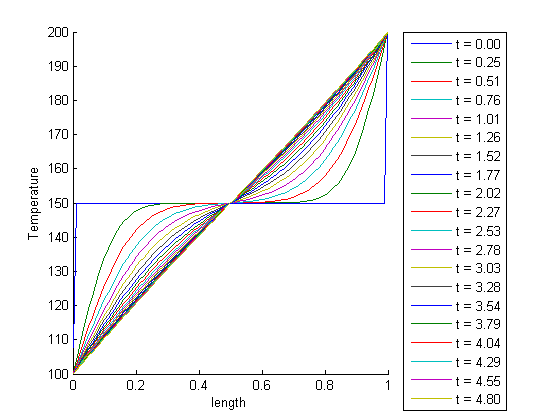
In Post 860 we solved a steady state BVP modeling heat conduction. Today we examine the transient behavior of a rod at constant T put between two heat reservoirs at different temperatures, again T1 = 100, and T2 = 200. The rod will start at 150. Over time, we should expect a solution that approaches the steady state solution: a linear temperature profile from one side of the rod to the other.

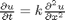
at 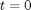, in this example we have 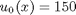as an initial condition. with boundary conditions 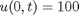and .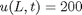

Matlab provides the pdepe command which can solve some PDEs. The syntax for the command is

 sol = pdepe(m,@pdex,@pdexic,@pdexbc,x,t)

where m is an integer that specifies the problem symmetry. The three function handles define the equations, initial conditions and boundary conditions. x and t are the grids to solve the PDE on.

function pdexfunc

close all; clc; clear all;

setup the problem

m=0; % specifies 1-D symmetry
x = linspace(0,1); % equally-spaced points along the length of the rod
t = linspace(0,5); % this creates time points

sol = pdepe(m,@pdex,@pdexic,@pdexbc,x,t);

plot the solution as a 3D surface

x is the position along the rod, t is the time sol is the temperature at (x,t)

surf(x,t,sol)
xlabel('Position')
ylabel('time')
zlabel('Temperature')

in the surface plot above you can see the approach from the initial conditions to the steady state solution.

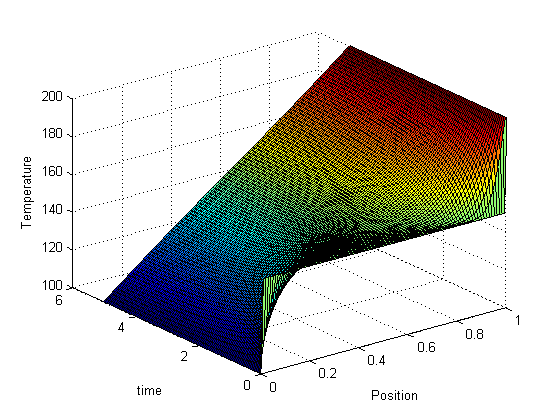
we can also plot the solutions in 2D, at different times. Our time vector has about 100 elements, so in this loop we plot every 5th time. We set a DisplayName in each plot so we can use them in the legend later.

figure
hold all % the use of all makes the colors cycle with each plot
for i=1:5:numel(t)
    plot(x,sol(i,:),'DisplayName',sprintf('t = %1.2f',t(i)))
end
xlabel('length')
ylabel('Temperature')

% we use -DynamicLegend to pick up the display names we set above.
legend('-DynamicLegend','location','bestoutside');
% this is not an easy way to see the solution.

animating the solution

we can create an animated gif to show how the solution evolves over time.

filename = 'animated-solution.gif'; % file to store image in
for i=1:numel(t)
    plot(x,sol(i,:));
    xlabel('Position')
    ylabel('Temperature')
    text(0.1,190,sprintf('t = %1.2f',t(i))); % add text annotation of time step
    frame = getframe(1);
    im = frame2im(frame); %convert frame to an image
    [imind,cm] = rgb2ind(im,256);

    % now we write out the image to the animated gif.
    if i == 1;
        imwrite(imind,cm,filename,'gif', 'Loopcount',inf);
    else
        imwrite(imind,cm,filename,'gif','WriteMode','append');
    end
end
close all; % makes sure the plot from the loop above doesn't get published

here is the animation!

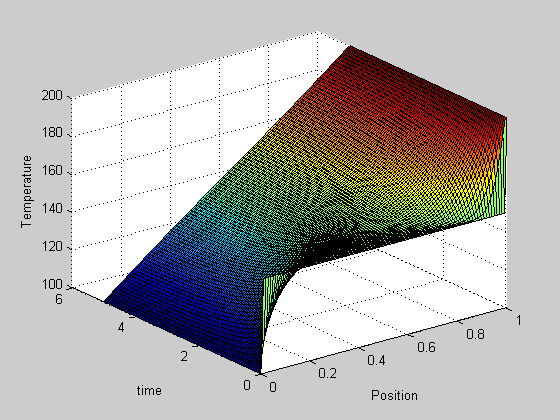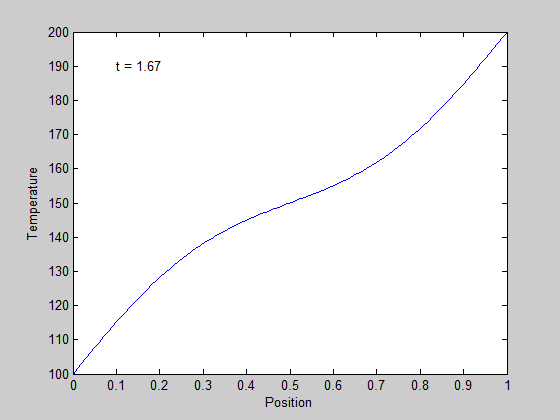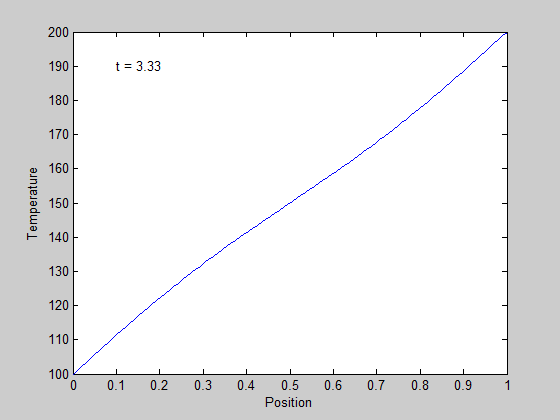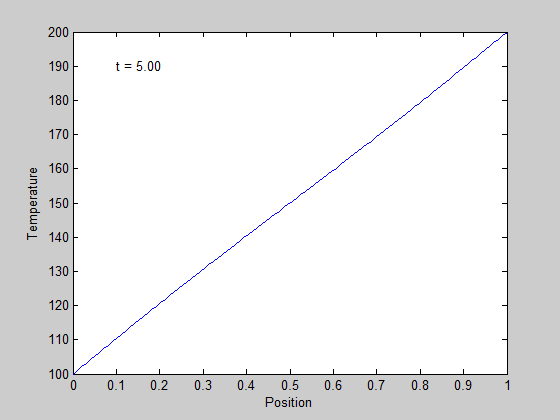
It is slightly more clear that the temperature profile evolves from a flat curve, to a linear temperature ramp between the two end points.

'done'

ans =

done

function [c,f,s] = pdex(x,t,u,DuDx)

For pdepe to understand the equations, they need to be in the form of

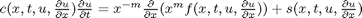
where c is a diagonal matrix, f is called a flux term, and s is the source term. Our equations are:

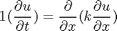
from which you can see that 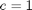, , and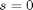

c = 1;
f = 0.02*DuDx;
s = 0;

function u0 = pdexic(x)
% this defines u(t=0) for all of x. The problem specifies a constant T for
% all of x.
u0 = 150;

function [p1,q1,pr,qr] = pdexbc(x1,u1,xr,ur,t)
% this defines the boundary conditions. The general form of the boundary
% conditions are $p(x,t,u) + q(x,t)f(x,t,u,\frac{\partial u}{\partial x})$
% We have to define the boundary conditions on the left, and right.
p1 = u1-100; % at left
q1 = 0; % at left
pr= ur-200;  % at right
qr = 0; % at right


% categories: PDEs
% tags: heat transfer

Published with MATLAB® 7.10