Gibbs energy minimization and the NIST webbook
December 26, 2011 at 01:10 AM | categories: optimization | View Comments
Gibbs energy minimization and the NIST webbook
John Kitchin
Contents
- Links to data
- We define species like this.
- Heats of formation at 298.15 K
- Shomate parameters for each species
- Shomate equations
- Gibbs energy of mixture
- Elemental conservation constraints
- Constraints on bounds
- Solve the minimization problem
- Compute mole fractions and partial pressures
- Computing equilibrium constants
In Post 1536 we used the NIST webbook to compute a temperature dependent Gibbs energy of reaction, and then used a reaction extent variable to compute the equilibrium concentrations of each species for the water gas shift reaction.
Today, we look at the direct minimization of the Gibbs free energy of the species, with no assumptions about stoichiometry of reactions. We only apply the constraint of conservation of atoms. We use the NIST Webbook to provide the data for the Gibbs energy of each species.
As a reminder we consider equilibrium between the species  ,
,  ,
, 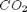 and
and 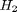 , at 1000K, and 10 atm total pressure with an initial equimolar molar flow rate of
, at 1000K, and 10 atm total pressure with an initial equimolar molar flow rate of  and
and  .
.
Links to data
function nist_wb_constrained_min
T = 1000; %K R = 8.314e-3; % kJ/mol/K P = 10; % atm, this is the total pressure in the reactor Po = 1; % atm, this is the standard state pressure
We define species like this.
We are going to store all the data and calculations in vectors, so we need to assign each position in the vector to a species. Here are the definitions we use in this work.
1 CO 2 H2O 3 CO2 4 H2
species = {'CO' 'H2O' 'CO2' 'H2'};
Heats of formation at 298.15 K
Hf298 = [
-110.53 % CO
-241.826 % H2O
-393.51 % CO2
0.0]; % H2
Shomate parameters for each species
A B C D E F G H
WB = [25.56759 6.096130 4.054656 -2.671301 0.131021 -118.0089 227.3665 -110.5271 % CO 30.09200 6.832514 6.793435 -2.534480 0.082139 -250.8810 223.3967 -241.8264 % H2O 24.99735 55.18696 -33.69137 7.948387 -0.136638 -403.6075 228.2431 -393.5224 % CO2 33.066178 -11.363417 11.432816 -2.772874 -0.158558 -9.980797 172.707974 0.0]; % H2
Shomate equations
t = T/1000; T_H = [t; t^2/2; t^3/3; t^4/4; -1/t; 1; 0; -1]; T_S = [log(t); t; t^2/2; t^3/3; -1/(2*t^2); 0; 1; 0]; H = WB*T_H; % (H - H_298.15) kJ/mol S = WB*T_S/1000; % absolute entropy kJ/mol/K Gjo = Hf298 + H - T*S; % Gibbs energy of each component at 1000 K
Gibbs energy of mixture
this function assumes the ideal gas law for the activities
function G = func(nj) Enj = sum(nj); G = sum(nj.*(Gjo'/R/T + log(nj/Enj*P/Po))); end
Elemental conservation constraints
We impose the constraint that all atoms are conserved from the initial conditions to the equilibrium distribution of species. These constraints are in the form of A_eq x = beq, where x is the vector of mole numbers. CO H2O CO2 H2
Aeq = [ 1 0 1 0 % C balance 1 1 2 0 % O balance 0 2 0 2]; % H balance % equimolar feed of 1 mol H2O and 1 mol CO beq = [1 % mol C fed 2 % mol O fed 2]; % mol H fed
Constraints on bounds
This simply ensures there are no negative mole numbers.
LB = [0 0 0];
Solve the minimization problem
x0 = [0.5 0.5 0.5 0.5]; % initial guesses options = optimset('Algorithm','sqp'); x = fmincon(@func,x0,[],[],Aeq,beq,LB,[],[],options)
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
x =
0.4549 0.4549 0.5451 0.5451
Compute mole fractions and partial pressures
The pressures here are in good agreement with the pressures found in Post 1536 . The minor disagreement (in the third or fourth decimal place) is likely due to convergence tolerances in the different algorithms used.
yj = x/sum(x); Pj = yj*P; for i=1:numel(x) fprintf('%5d%10s%15.4f atm\n',i, species{i}, Pj(i)) end
1 CO 2.2745 atm
2 H2O 2.2745 atm
3 CO2 2.7255 atm
4 H2 2.7255 atm
Computing equilibrium constants
We can compute the equilibrium constant for the reaction 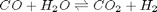 . Compared to the value of K = 1.44 we found at the end of Post 1536 , the agreement is excellent. Note, that to define an equilibrium constant it is necessary to specify a reaction, even though it is not necessary to even consider a reaction to obtain the equilibrium distribution of species!
. Compared to the value of K = 1.44 we found at the end of Post 1536 , the agreement is excellent. Note, that to define an equilibrium constant it is necessary to specify a reaction, even though it is not necessary to even consider a reaction to obtain the equilibrium distribution of species!
nuj = [-1 -1 1 1]; % stoichiometric coefficients of the reaction
K = prod(yj.^nuj)
K =
1.4359
end % categories: optimization % tags: Thermodynamics, reaction engineering
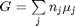 . Recalling that we define
. Recalling that we define 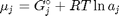 , and in the ideal gas limit,
, and in the ideal gas limit, 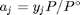 , and that
, and that 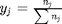 . Since in this problem, P = 1 atm, this leads to the function
. Since in this problem, P = 1 atm, this leads to the function 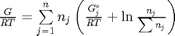 .
.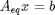 where
where  is a vector of the moles of each species present in the mixture. CH4 C2H4 C2H2 CO2 CO O2 H2 H2O C2H6
is a vector of the moles of each species present in the mixture. CH4 C2H4 C2H2 CO2 CO O2 H2 H2O C2H6 . Even though nearly all the ethane is consumed, we don't get the full yield of hydrogen. It appears that another equilibrium, one between CO, CO2, H2O and H2, may be limiting that, since the rest of the hydrogen is largely in the water. It is also of great importance that we have not said anything about reactions, i.e. how these products were formed. This is in stark contrast to
. Even though nearly all the ethane is consumed, we don't get the full yield of hydrogen. It appears that another equilibrium, one between CO, CO2, H2O and H2, may be limiting that, since the rest of the hydrogen is largely in the water. It is also of great importance that we have not said anything about reactions, i.e. how these products were formed. This is in stark contrast to 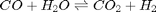 . We can compute the Gibbs free energy of the reaction from the heats of formation of each species. Assuming these are the formation energies at 1000K, this is the reaction free energy at 1000K.
. We can compute the Gibbs free energy of the reaction from the heats of formation of each species. Assuming these are the formation energies at 1000K, this is the reaction free energy at 1000K. subject to the constraint that
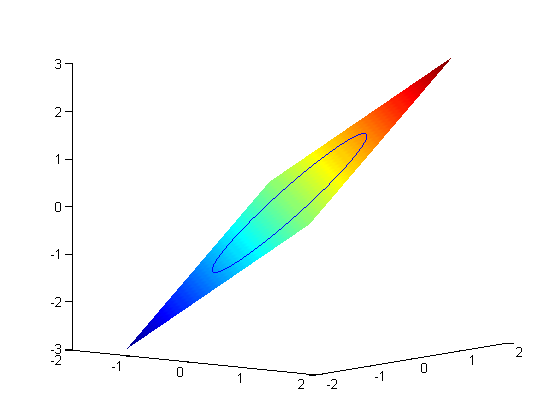
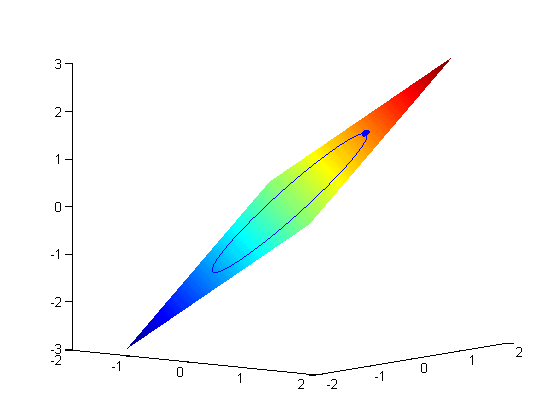
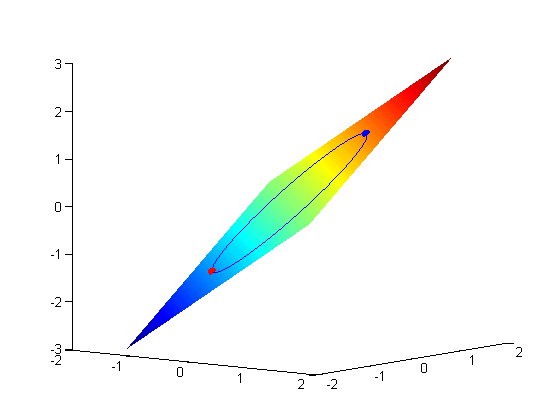
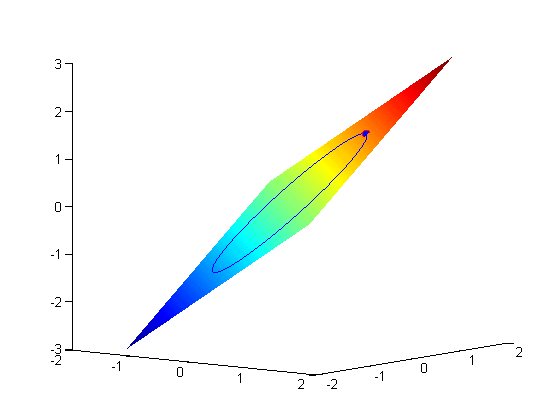
subject to the constraint that 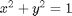 . The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. In
. The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. In 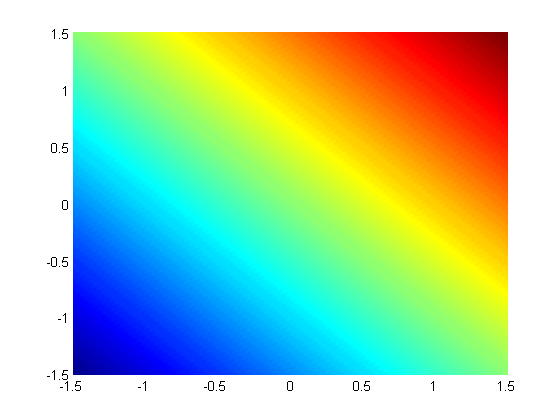
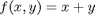 subject to the constraint that
subject to the constraint that 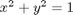 . The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. We plot these two functions here.
. The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. We plot these two functions here.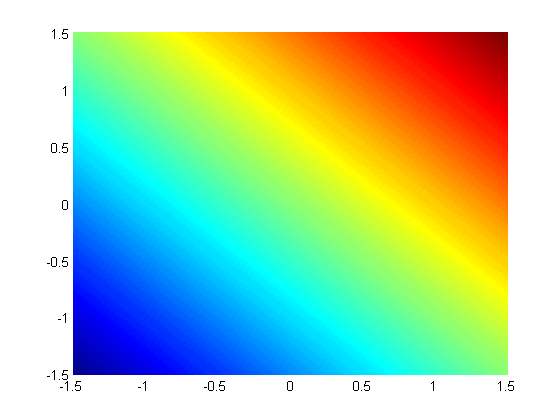
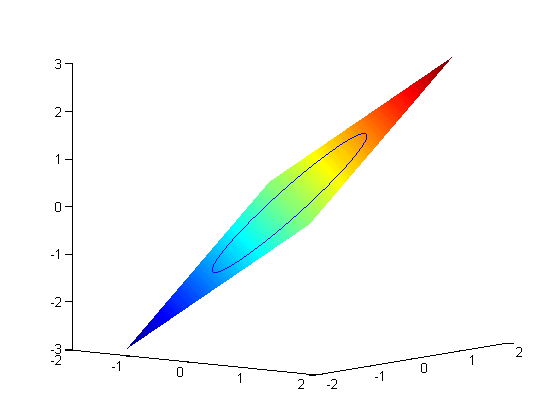
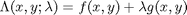 where
where 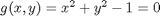 , which is the constraint function. Since
, which is the constraint function. Since 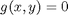 , we aren't really changing the original function, provided that the constraint is met!
, we aren't really changing the original function, provided that the constraint is met!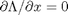 ,
, 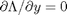 , and
, and 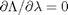 . the process for solving this is usually to analytically evaluate the partial derivatives, and then solve the unconstrained resulting equations, which may be nonlinear.
. the process for solving this is usually to analytically evaluate the partial derivatives, and then solve the unconstrained resulting equations, which may be nonlinear.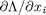 .
.
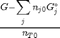
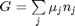 where
where 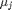 is the chemical potential of species
is the chemical potential of species  , and it is temperature and pressure dependent, and
, and it is temperature and pressure dependent, and 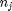 is the number of moles of species
is the number of moles of species 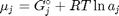 , where
, where 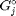 is the Gibbs energy in a standard state, and
is the Gibbs energy in a standard state, and  is the activity of species
is the activity of species  and stoichiometric coefficients:
and stoichiometric coefficients: 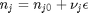 . Note that the reaction extent has units of moles.
. Note that the reaction extent has units of moles.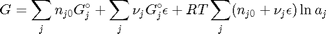
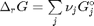 . With these observations we rewrite the equation as:
. With these observations we rewrite the equation as: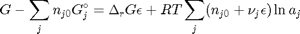
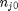 . It is desirable to avoid this, so we now rescale the equation by the total initial moles present,
. It is desirable to avoid this, so we now rescale the equation by the total initial moles present, 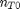 and define a new variable
and define a new variable 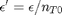 , which is dimensionless. This leads to:
, which is dimensionless. This leads to: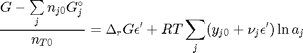
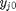 is the initial mole fraction of species
is the initial mole fraction of species 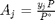 , where the numerator is the partial pressure of species
, where the numerator is the partial pressure of species 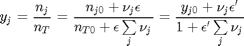
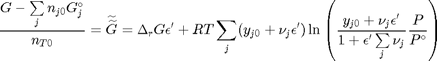
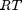 . This additional scaling makes the quantities dimensionless, and makes the quantity have a magnitude of order unity, but otherwise has no effect on the shape of the graph.
. This additional scaling makes the quantities dimensionless, and makes the quantity have a magnitude of order unity, but otherwise has no effect on the shape of the graph.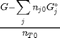
 can be. Recall that
can be. Recall that 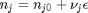 , and that
, and that 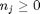 . Thus,
. Thus, 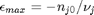 , and the maximum value that
, and the maximum value that 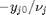 where
where 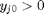 . When there are multiple species, you need the smallest
. When there are multiple species, you need the smallest 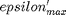 to avoid getting negative mole numbers.
to avoid getting negative mole numbers.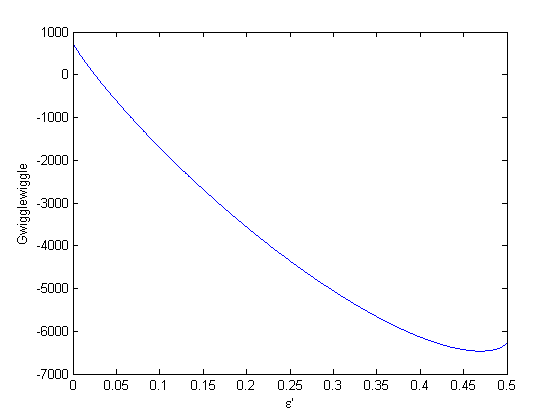
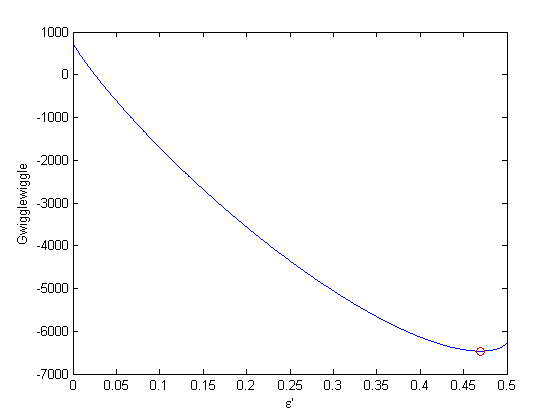
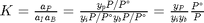 .
.