On the quad, or trapz'd in ChemE heaven?
September 13, 2011 at 01:47 AM | categories: basic matlab | View Comments
Contents
On the quad, or trapz'd in ChemE heaven?
John Kitchin
What is the difference between quad and trapz? The short answer is that quad integrates functions (via a function handle) using numerical quadrature, and trapz performs integration of arrays of data using the trapezoid method.
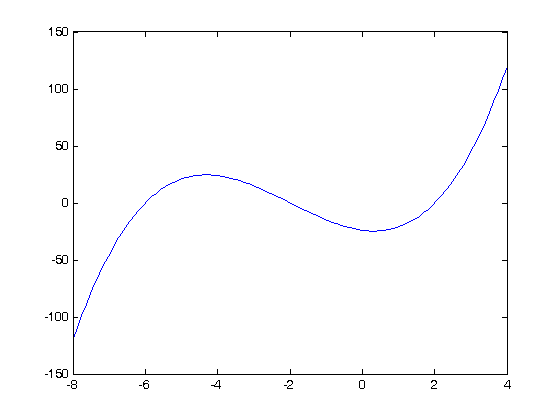
Let's look at some examples. We consider the example of computing 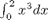 . the analytical integral is
. the analytical integral is 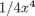 , so we know the integral evaluates to 16/4 = 4. This will be our benchmark for comparison to the numerical methods.
, so we know the integral evaluates to 16/4 = 4. This will be our benchmark for comparison to the numerical methods.
clear all; clc; close all;
quad usage
This command is equivalent to 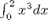
i1 = quad(@(x) x.^3,0,2)
i1 =
4
we can also define the function handle separately.
f = @(x) x.^3
f(2) % should be 8
f =
@(x)x.^3
ans =
8
This command is equivalent to 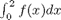
i1 = quad(f,0,2)
error = (i1 - 4)/4
% Note the error is very small!
i1 =
4
error =
0
Trapz usage
if we had numerical data like this, we use trapz to integrate it
x = [0 0.5 1 1.5 2];
y = f(x); % or you could say y = x.^3
i2 = trapz(x,y)
error = (i2 - 4)/4
i2 =
4.2500
error =
0.0625
Note the integral of these vectors is greater than 4! You can see why here.
figure; hold all plot(x,y) ezplot(f,[0 2]) legend 'numerical data' 'analytical function' % The area of the trapezoids is greater than the area under the function % due to the coarse sampling of $f(x)=x^3$.
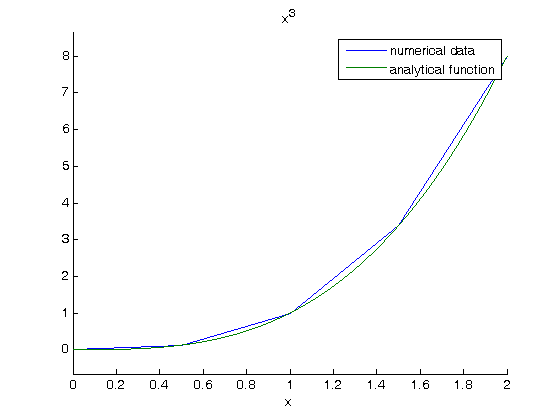
with a finer sampling we have:
x = linspace(0,2); % 100 points between 0, 1
y = x.^3;
i3 = trapz(x,y)
i3 =
4.0004
and a much smaller error.
error = (i3 - 4)/4
error = 1.0203e-004
Combining numerical data with quad
You might want to combine numerical data with the quad function if you want to perform integrals easily. Let's say you are given this data:
x = [0 0.5 1 1.5 2]; y = [0 0.1250 1.0000 3.3750 8.0000];
and you want to integrate this from x = 0.25 to 1.75. We don't have data in those regions, so some interpolation is going to be needed. Here is the analytical integral and by numerical quadrature
i_analytical = 1/4*(1.75^4-0.25^4)
i = quad(f,0.25,1.75)
% they are practically the same.
i_analytical =
2.3438
i =
2.3437
One way to do this with the data provided is to use interpolation on a fine-spaced x-grid, and then use trapz on the resulting interpolated vectors.
xfine = linspace(0.25,1.75); yinterp = interp1(x,y,xfine); i4 = trapz(xfine,yinterp) error = (i4 - i_analytical)/i_analytical
i4 =
2.5315
error =
0.0801
Another approach is to create a function handle to do the interpolation for you. This combines numerical data with the quad function!
finterp = @(X) interp1(x,y,X); i5 = quad(finterp,0.25,1.75) error = (i5 - i_analytical)/i_analytical
i5 =
2.5312
error =
0.0800
these two approaches are actually identical, as they are both based on linear interpolation. The second approach is slightly more compact and easier to evaluate multiple integrals. Compare:
i6 = quad(finterp,0.28,1.64)
i6 =
1.9596
to:
xfine = linspace(0.28,1.64);
yinterp = interp1(x,y,xfine);
i7 = trapz(xfine,yinterp)
% One line of code vs. three.
i7 =
1.9597
Summary
trapz and quad are functions for getting integrals. Both can be used with numerical data if interpolation is used.
Finally, see this post for an example of solving an integral equation using quad and fsolve.
% categories: basic matlab % tags: integration
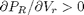 , the isotherm fails to describe real materials, which phase separate into a liquid and gas in this region.
, the isotherm fails to describe real materials, which phase separate into a liquid and gas in this region.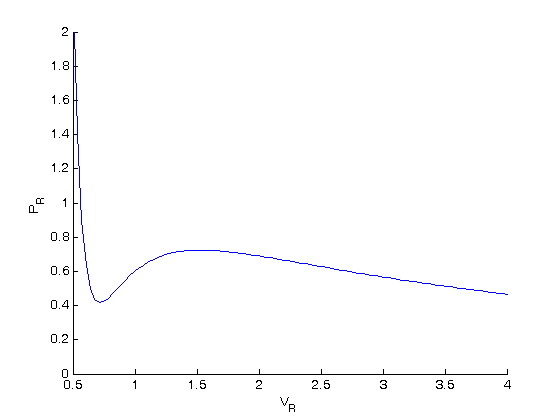
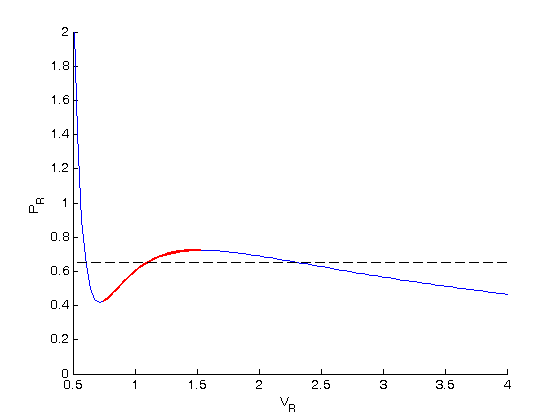
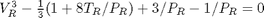 . We use the coefficients t0 get the rooys like this.
. We use the coefficients t0 get the rooys like this.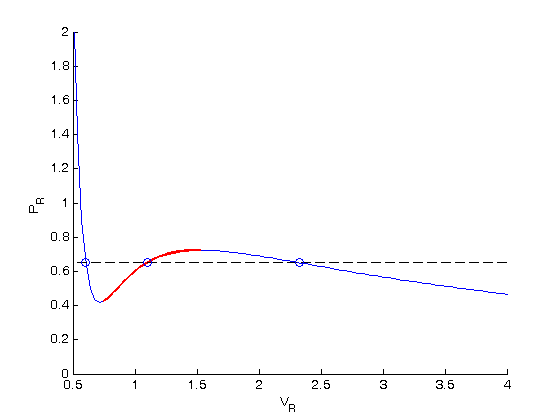
 . We use logical indexing to select the parts of the data that we want.
. We use logical indexing to select the parts of the data that we want.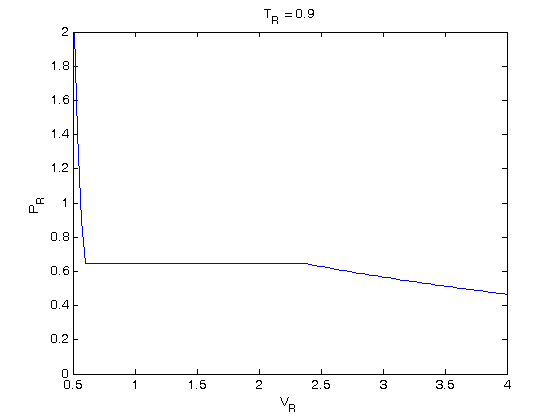
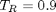 . You could also compute the isotherm for other
. You could also compute the isotherm for other 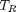 values.
values.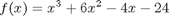
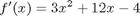
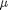 between two stationary plates separated by distance
between two stationary plates separated by distance 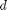 and driven by a pressure drop
and driven by a pressure drop 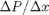 , the governing equations on the velocity
, the governing equations on the velocity  of the fluid are (assuming flow in the x-direction with the velocity varying only in the y-direction):
of the fluid are (assuming flow in the x-direction with the velocity varying only in the y-direction):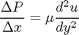
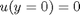 and
and 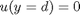 , i.e. the no-slip condition at the edges of the plate.
, i.e. the no-slip condition at the edges of the plate.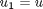 ,
, 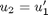 and then
and then 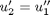 . This leads to:
. This leads to: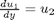
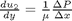
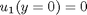 and
and 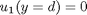 .
.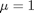 , and
, and  .
.