Counting roots

John Kitchin

Contents

Problem statement

The goal here is to determine how many roots there are in a nonlinear function we are interested in solving. For this example, we use a cubic polynomial because we know there are three roots.

function main

clc; clear all; close all;

Use roots for this polynomial

This ony works for a polynomial, it does not work for any other nonlinear function.

roots([1 6 -4 -24])

ans =

   -6.0000
    2.0000
   -2.0000

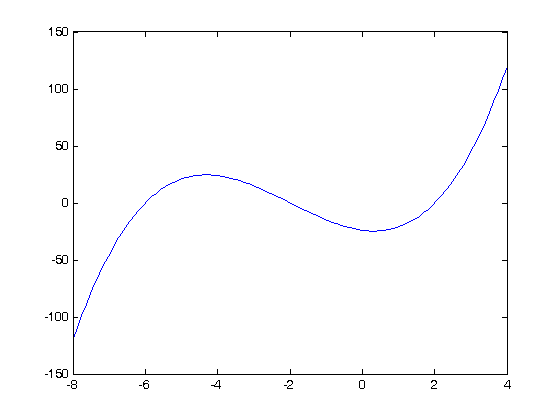
Plot the function to see where the roots are

x = linspace(-8,4);
fx = x.^3 + 6*x.^2 - 4*x - 24;
plot(x,fx)

method 1

count the number of times the sign changes in the interval. We determine the sign of each element (-1, 0 or +1) and then use a a loop to go through each element. A sign change is detected when an element is not equal to the previous element. Note this is not foolproof; we may over count roots if we get a sequence -1 0 1. We check for that by making sure neither of the two elements being compared are zero.

sign_fx = sign(fx);

count = 0;
for i=2:length(sign_fx)
    if sign_fx(i) ~= sign_fx(i-1) && sign_fx(i) ~= 0 && sign_fx(i-1) ~= 0
        count = count + 1;
        disp(sprintf('A root is between x = %f and %f',x(i-1),x(i)))
    end
end

disp(sprintf('The number of sign changes is %i.',count))

A root is between x = -6.060606 and -5.939394
A root is between x = -2.060606 and -1.939394
A root is between x = 1.939394 and 2.060606
The number of sign changes is 3.

method 1a

this one line code also counts sign changes. the diff command makes all adjacent, identical elements equal zero, and sign changes = 2 (1 - (-1)) or (-1 - 1). Then we just sum up the diff vector, divide by two, and that is the number of roots. Note that no check for 0 is needed; you will get 1/2 a sign change from -1 to 0. and another half from 0 to 1. They add up to a whole sign change.

sum(abs(diff(sign_fx))/2)

ans =

     3

Discussion

Method 1 is functional but requires some programming. Method 1a is concise but probably tricky to remember.

Method 2

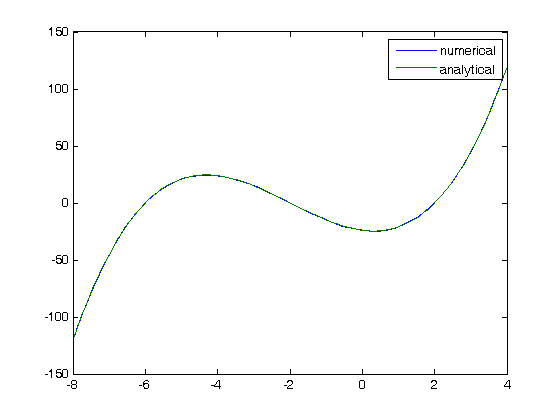
using events in an ODE solver Matlab can identify events in the solution to an ODE, for example, when a function has a certain value, e.g. f(x) = 0. We can take advantage of this to find the roots and number of roots in this case.

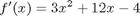
with f(-8) = -120

xspan = [-8 4];
fp0 = -120;

options = odeset('Events',@event_function);
[X,Y,XE,VE,IE] = ode45(@myode,xspan,fp0,options);
XE % these are the x-values where the function equals zero
nroots = length(XE);
disp(sprintf('Found %i roots in the x interval',nroots))

% lets compare the solution to the  original function to make sure they are
% the same.
figure
plot(X,Y,x,fx)
legend 'numerical' 'analytical'

function dfdx = myode(x,f)
dfdx = 3*x^2 + 12*x - 4;

function [value,isterminal,direction] = event_function(t,y)
value = y - 0;  % then value = 0, an event is triggered
isterminal = 0; % do not terminate after the first event
direction = 0;  % get all the zeros

% categories: ODEs, nonlinear algebra

XE =

   -6.0000
   -2.0000
    2.0000

Found 3 roots in the x interval

Published with MATLAB® 7.10