Water gas shift equilibria via the NIST Webbook
John Kitchin
The NIST webbook provides parameterized models of the enthalpy, entropy and heat capacity of many molecules. In this example, we will examine how to use these to compute the equilibrium constant for the water gas shift reaction 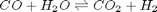 in the temperature range of 500K to 1000K.
in the temperature range of 500K to 1000K.
Parameters are provided for:
Contents
Cp = heat capacity (J/mol*K)
H° = standard enthalpy (kJ/mol)
S° = standard entropy (J/mol*K)
with models in the form: 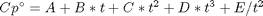
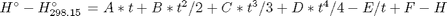
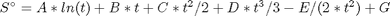
where  , and
, and  is the temperature in Kelvin. We can use this data to calculate equilibrium constants in the following manner. First, we have heats of formation at standard state for each compound; for elements, these are zero by definition, and for non-elements, they have values available from the NIST webbook. There are also values for the absolute entropy at standard state. Then, we have an expression for the change in enthalpy from standard state as defined above, as well as the absolute entropy. From these we can derive the reaction enthalpy, free energy and entropy at standard state, as well as at other temperatures.
is the temperature in Kelvin. We can use this data to calculate equilibrium constants in the following manner. First, we have heats of formation at standard state for each compound; for elements, these are zero by definition, and for non-elements, they have values available from the NIST webbook. There are also values for the absolute entropy at standard state. Then, we have an expression for the change in enthalpy from standard state as defined above, as well as the absolute entropy. From these we can derive the reaction enthalpy, free energy and entropy at standard state, as well as at other temperatures.
We will examine the water gas shift enthalpy, free energy and equilibrium constant from 500K to 1000K, and finally compute the equilibrium composition of a gas feed containing 5 atm of CO and H2 at 1000K.
close all; clear all; clc;
T = linspace(500,1000);
t = T/1000;
Setup equations for each species
First we enter in the parameters and compute the enthalpy and entropy for each species.
Hydrogen
link
A = 33.066178;
B = -11.363417;
C = 11.432816;
D = -2.772874;
E = -0.158558;
F = -9.980797;
G = 172.707974;
H = 0.0;
Hf_29815_H2 = 0.0;
S_29815_H2 = 130.68;
dH_H2 = A*t + B*t.^2/2 + C*t.^3/3 + D*t.^4/4 - E./t + F - H;
S_H2 = (A*log(t) + B*t + C*t.^2/2 + D*t.^3/3 - E./(2*t.^2) + G);
H2O
link Note these parameters limit the temperature range we can examine, as these parameters are not valid below 500K. There is another set of parameters for lower temperatures, but we do not consider them here.
A = 30.09200;
B = 6.832514;
C = 6.793435;
D = -2.534480;
E = 0.082139;
F = -250.8810;
G = 223.3967;
H = -241.8264;
Hf_29815_H2O = -241.83;
S_29815_H2O = 188.84;
dH_H2O = A*t + B*t.^2/2 + C*t.^3/3 + D*t.^4/4 - E./t + F - H;
S_H2O = (A*log(t) + B*t + C*t.^2/2 + D*t.^3/3 - E./(2*t.^2) + G);
CO
link
A = 25.56759;
B = 6.096130;
C = 4.054656;
D = -2.671301;
E = 0.131021;
F = -118.0089;
G = 227.3665;
H = -110.5271;
Hf_29815_CO = -110.53;
S_29815_CO = 197.66;
dH_CO = A*t + B*t.^2/2 + C*t.^3/3 + D*t.^4/4 - E./t + F - H;
S_CO = (A*log(t) + B*t + C*t.^2/2 + D*t.^3/3 - E./(2*t.^2) + G);
CO2
link
A = 24.99735;
B = 55.18696;
C = -33.69137;
D = 7.948387;
E = -0.136638;
F = -403.6075;
G = 228.2431;
H = -393.5224;
Hf_29815_CO2 = -393.51;
S_29815_CO2 = 213.79;
dH_CO2 = A*t + B*t.^2/2 + C*t.^3/3 + D*t.^4/4 - E./t + F - H;
S_CO2 = (A*log(t) + B*t + C*t.^2/2 + D*t.^3/3 - E./(2*t.^2) + G);
Standard state heat of reaction
We compute the enthalpy and free energy of reaction at 298.15 K for the following reaction 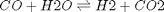 .
.
Hrxn_29815 = Hf_29815_CO2 + Hf_29815_H2 - Hf_29815_CO - Hf_29815_H2O;
Srxn_29815 = S_29815_CO2 + S_29815_H2 - S_29815_CO - S_29815_H2O;
Grxn_29815 = Hrxn_29815 - 298.15*(Srxn_29815)/1000;
sprintf('deltaH = %1.2f',Hrxn_29815)
sprintf('deltaG = %1.2f',Grxn_29815)
ans =
deltaH = -41.15
ans =
deltaG = -28.62
Correcting 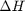 and
and 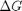
we have to correct for temperature change away from standard state. We only correct the enthalpy for this temperature change. The correction looks like this:
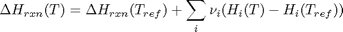
Where 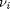 are the stoichiometric coefficients of each species, with appropriate sign for reactants and products, and
are the stoichiometric coefficients of each species, with appropriate sign for reactants and products, and 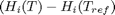 is precisely what is calculated for each species with the equations
is precisely what is calculated for each species with the equations
Hrxn = Hrxn_29815 + dH_CO2 + dH_H2 - dH_CO - dH_H2O;
The entropy is on an absolute scale, so we directly calculate entropy at each temperature. Recall that H is in kJ/mol and S is in J/mol/K, so we divide S by 1000 to make the units match.
Grxn = Hrxn - T.*(S_CO2 + S_H2 - S_CO - S_H2O)/1000;
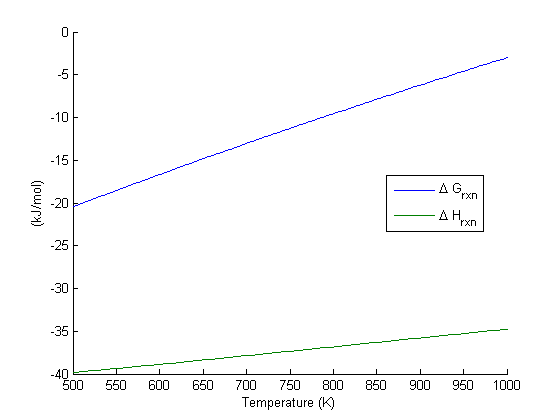
Plot how the 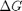 varies with temperature
varies with temperature
over this temperature range the reaction is exothermic, although near 1000K it is just barely exothermic. At higher temperatures we expect the reaction to become endothermic.
figure; hold all
plot(T,Grxn)
plot(T,Hrxn)
xlabel('Temperature (K)')
ylabel('(kJ/mol)')
legend('\Delta G_{rxn}', '\Delta H_{rxn}', 'location','best')
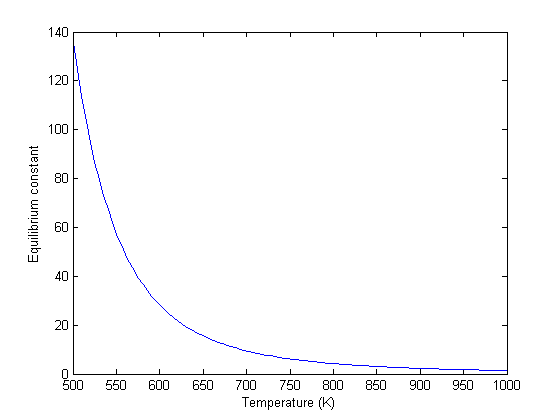
Equilibrium constant calculation
Note the equilibrium constant starts out high, i.e. strongly favoring the formation of products, but drops very quicky with increasing temperature.
R = 8.314e-3;
K = exp(-Grxn/R./T);
figure
plot(T,K)
xlim([500 1000])
xlabel('Temperature (K)')
ylabel('Equilibrium constant')
Equilibrium yield of WGS
Now let's suppose we have a reactor with a feed of H2O and CO at 10atm at 1000K. What is the equilibrium yield of H2? Let  be the extent of reaction, so that
be the extent of reaction, so that 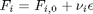 . For reactants,
. For reactants, 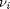 is negative, and for products,
is negative, and for products, 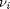 is positive. We have to solve for the extent of reaction that satisfies the equilibrium condition.
is positive. We have to solve for the extent of reaction that satisfies the equilibrium condition.
A = CO
B = H2O
C = H2
D = CO2
Pa0 = 5; Pb0 = 5; Pc0 = 0; Pd0 = 0;
R = 0.082;
Temperature = 1000;
K_Temperature = interp1(T,K,Temperature);
f = @(X) K_Temperature - X^2/(1-X)^2;
Xeq = fzero(f,[1e-3 0.999]);
sprintf('The equilibrium conversion for these feed conditions is: %1.2f',Xeq)
ans =
The equilibrium conversion for these feed conditions is: 0.55
Compute gas phase pressures of each species
Since there is no change in moles for this reaction, we can directly calculation the pressures from the equilibrium conversion and the initial pressure of gases. you can see there is a slightly higher pressure of H2 and CO2 than the reactants, consistent with the equilibrium constant of about 1.44 at 1000K. At a lower temperature there would be a much higher yield of the products. For example, at 550K the equilibrium constant is about 58, and the pressure of H2 is 4.4 atm due to a much higher equilibrium conversion of 0.88.
P_CO = Pa0*(1-Xeq)
P_H2O = Pa0*(1-Xeq)
P_H2 = Pa0*Xeq
P_CO2 = Pa0*Xeq
P_CO =
2.2748
P_H2O =
2.2748
P_H2 =
2.7252
P_CO2 =
2.7252
Compare the equilibrium constants
We can compare the equilibrium constant from the Gibbs free energy and the one from the ratio of pressures. They should be the same!
K_Temperature
(P_CO2*P_H2)/(P_CO*P_H2O)
K_Temperature =
1.4352
ans =
1.4352
Summary
The NIST Webbook provides a plethora of data for computing thermodynamic properties. It is a little tedious to enter it all into Matlab, and a little tricky to use the data to estimate temperature dependent reaction energies. A limitation of the Webbook is that it does not tell you have the thermodynamic properties change with pressure. Luckily, those changes tend to be small.
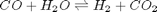 . We can illustrate the conservation of mass with the following equation:
. We can illustrate the conservation of mass with the following equation:  . Where
. Where  is the stoichiometric coefficient vector and
is the stoichiometric coefficient vector and  is a column vector of molecular weights. For simplicity, we use pure isotope molecular weights, and not the isotope-weighted molecular weights.
is a column vector of molecular weights. For simplicity, we use pure isotope molecular weights, and not the isotope-weighted molecular weights.
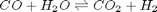 in the temperature range of 500K to 1000K.
in the temperature range of 500K to 1000K. and
and 
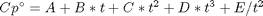
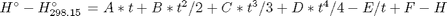
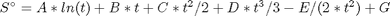
 , and
, and 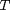 is the temperature in Kelvin. We can use this data to calculate equilibrium constants in the following manner. First, we have heats of formation at standard state for each compound; for elements, these are zero by definition, and for non-elements, they have values available from the NIST webbook. There are also values for the absolute entropy at standard state. Then, we have an expression for the change in enthalpy from standard state as defined above, as well as the absolute entropy. From these we can derive the reaction enthalpy, free energy and entropy at standard state, as well as at other temperatures.
is the temperature in Kelvin. We can use this data to calculate equilibrium constants in the following manner. First, we have heats of formation at standard state for each compound; for elements, these are zero by definition, and for non-elements, they have values available from the NIST webbook. There are also values for the absolute entropy at standard state. Then, we have an expression for the change in enthalpy from standard state as defined above, as well as the absolute entropy. From these we can derive the reaction enthalpy, free energy and entropy at standard state, as well as at other temperatures.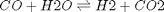 .
. and
and 
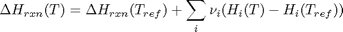
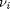 are the stoichiometric coefficients of each species, with appropriate sign for reactants and products, and
are the stoichiometric coefficients of each species, with appropriate sign for reactants and products, and 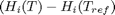 is precisely what is calculated for each species with the equations
is precisely what is calculated for each species with the equations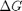 varies with temperature
varies with temperature

 be the extent of reaction, so that
be the extent of reaction, so that 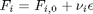 . For reactants,
. For reactants, 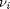 is negative, and for products,
is negative, and for products,