Contents

Issues with nested functions

John Kitchin

Nested functions are great for passing lots of information between functions conveniently. But, there are some gotchas to be wary of!

function main

a typical nested function use

It is common to define several parameters, and then to use them inside a nested function

a = 4;
b = 3;

    function y = f1(x)
        y = a + b*x;
    end

f1(2)

ans =

    10

classic example of a potential problem

Nested functions share the same namespace as the main function, which means you can change the value of a variable in the main function in the nested function. This does not happen with subfunctions.

i = 5 % initial value of i
    function y = f2(x)
        % nested function that uses a and b from above, and uses an
        % internal loop to compute a value of y.
        y = 0;
        for i=1:10  % this is going to change the value of i outside this function
            y = y + a*b + i;
        end
    end

f2(2)
i % note i = 10 now

i =

     5


ans =

   175


i =

    10

This kind of behavior can be very difficult to debug or even know is a problem! you have to be aware that it is an issue when using nested functions.

subfunctions

subfunctions do not share namespaces, so you can reuse variable names. This can prevent accidental variable value changes, but, you have to put the variable information into the subfunction

i = 5
f3(2)
i % note that the value of i has not been changed here.

i =

     5


ans =

   175


i =

     5

end

function y = f3(x)
% subfunction that uses a and b from above, and uses an internal loop
% to compute a value of y.
a = 4;
b = 3;
y = 0;
for i=1:10  % this is going to change the value of i outside this function
    y = y + a*b + i;
end
end

% categories: basic

Published with MATLAB® 7.12

Contents

Estimating the boiling point of water

John Kitchin

I got distracted looking for Shomate parameters for ethane today, and came across this website on predicting the boiling point of water using the Shomate equations. The basic idea is to find the temperature where the Gibbs energy of water as a vapor is equal to the Gibbs energy of the liquid.

clear all; close all

Liquid water

http://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185&Units=SI&Mask=2#Thermo-Condensed valid over 298-500

Hf_liq = -285.830; % kJ/mol
S_liq = 0.06995;   % kJ/mol/K
shomateL = [-203.6060
            1523.290
           -3196.413
            2474.455
               3.855326
            -256.5478
            -488.7163
            -285.8304];

Gas phase water

http://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185&Units=SI&Mask=1&Type=JANAFG&Table=on#JANAFG

Interestingly, these parameters are listed as valid only above 500K. That means we have to extrapolate the values down to 298K. That is risky for polynomial models, as they can deviate substantially outside the region they were fitted to.

Hf_gas = -241.826; % kJ/mol
S_gas = 0.188835;  % kJ/mol/K

shomateG = [30.09200
             6.832514
             6.793435
            -2.534480
             0.082139
          -250.8810
           223.3967
          -241.8264];

Compute G over a range of temperatures.

T = linspace(0,200)' + 273.15; % temperature range from 0 to 200 degC

t = T/1000;

% normalize sTT by 1/1000  so entropies are in kJ/mol/K
sTT = [log(t) t t.^2/2 t.^3/3 -1./(2*t.^2) 0*t.^0 t.^0 0*t.^0]/1000;
hTT = [t t.^2/2 t.^3/3 t.^4/4 -1./t 1*t.^0 0*t.^0 -1*t.^0];

Gliq = Hf_liq + hTT*shomateL - T.*(sTT*shomateL);
Ggas = Hf_gas + hTT*shomateG - T.*(sTT*shomateG);

Interpolate the difference between the two vectors to find the boiling point

The boiling point is where Gliq = Ggas, so we solve Gliq(T)-Ggas(T)=0 to find the point where the two free energies are equal.

f = @(t) interp1(T,Gliq-Ggas,t);
bp = fzero(f,373)

bp =

  373.2045

Plot the two free energies

You can see the intersection occurs at approximately 100 degC.

plot(T-273.15,Gliq,T-273.15,Ggas)
line([bp bp]-273.15,[min(Gliq) max(Gliq)])
legend('liquid water','steam')
xlabel('Temperature \circC')
ylabel('\DeltaG (kJ/mol)')
title(sprintf('The boiling point is approximately %1.2f \\circC', bp-273.15))

Summary

The answer we get us 0.05 K too high, which is not bad considering we estimated it using parameters that were fitted to thermodynamic data and that had finite precision and extrapolated the steam properties below the region the parameters were stated to be valid for.

% tags: thermodynamics

Published with MATLAB® 7.13

Conservation of mass in chemical reactions

John Kitchin

Atoms cannot be destroyed in non-nuclear chemical reactions, hence it follows that the same number of atoms entering a reactor must also leave the reactor. The atoms may leave the reactor in a different molecular configuration due to the reaction, but the total mass leaving the reactor must be the same. Here we look at a few ways to show this.

Contents

Water gas shift reaction

We consider the water gas shift reaction : % . We can illustrate the conservation of mass with the following equation: 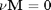. Where is the stoichiometric coefficient vector and 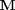is a column vector of molecular weights. For simplicity, we use pure isotope molecular weights, and not the isotope-weighted molecular weights.

nu = [-1 -1 1 1];
M = [28; 18; 2; 44];
nu*M

ans =

     0

Atomic mass balances

For any balanced chemical equation, there are the same number of each kind of atom on each side of the equation. Since the mass of each atom is unchanged with reaction, that means the mass of all the species that are reactants must equal the mass of all the species that are products! Here we look at the n C O H

reactants = [-1 -2 -2]
products  = [ 1  2  2]
M = [12.011; 15.999; 1.0079]

reactants =

    -1    -2    -2


products =

     1     2     2


M =

   12.0110
   15.9990
    1.0079

Now if we add the mass of reactants and products, it should sum to zero (since we used the negative sign for stoichiometric coefficients of reactants).

products*M + reactants*M

ans =

     0

Summary

That's all there is to mass conservation with reactions. Nothing changes if there are lots of reactions, as long as each reaction is properly balanced, and none of them are nuclear reactions!

tags: reaction engineering

Published with MATLAB® 7.12

Some basic data structures in Matlab

John Kitchin

There are a variety of needs for storing complicated data in solving engineering problems.

Contents

cell arrays

A cell array can store a variety of data types. A cell array is enclosed by curly brackets. Here, we might store the following data in a variable to describe the Antoine coefficients for benzene and the range they are relevant for [Tmin Tmax]

c = {'benzene' 6.9056 1211.0 220.79 [-16 104]}

c = 

    'benzene'    [6.9056]    [1211]    [220.7900]    [1x2 double]

To access the elements of a cell array use curly brackets for indexing.

c{1}

ans =

benzene

you can also index the cell array, e.g. to get elements 2-4:

[A B C] = c{2:4}

A =

    6.9056


B =

        1211


C =

  220.7900

If you want to extract all the contents to variable names that are easy to read, use this syntax:

[name A B C Trange] = c{:}

name =

benzene


A =

    6.9056


B =

        1211


C =

  220.7900


Trange =

   -16   104

structures

a structure contains named fields that can contain a variety of data types. Structures are often used to set options

s = struct('name','benzene','A',6.9056,'B',1211.0')

s = 

    name: 'benzene'
       A: 6.9056
       B: 1211

And you can add fields like this:

s.C = 220.79
s.Trange = [-16 104]

s = 

    name: 'benzene'
       A: 6.9056
       B: 1211
       C: 220.7900


s = 

      name: 'benzene'
         A: 6.9056
         B: 1211
         C: 220.7900
    Trange: [-16 104]

we can access the data in a struct by the field

s.name
s.Trange

ans =

benzene


ans =

   -16   104

It is an error to access a non-existent field, so you can check if it exists like this.

if isfield(s,'field3')
    s.field3
else
    'no field 3 found'
end

ans =

no field 3 found

Not sure what fields are in the struct? This might be the case for a struct returned by a Matlab function, e.g. by an ode solver or optimization algorithm.

fieldnames(s)

ans = 

    'name'
    'A'
    'B'
    'C'
    'Trange'

containers.Map

A container.Map is like a dictionary, with a key:value relationship. You can use complicated key strings including spaces. By default, all keys must be the same type, e.g. all strings.

cM = containers.Map();
cM('name') = 'benzene';
cM('A') = 6.9056;
cM('B') = 1211.0;
cM('C') = 220.79;
cM('Trange') = [-16 104];
cM('key with spaces') = 'random thoughts';

and we can access the data in a map by key:

cM('name')
cM('key with spaces')

ans =

benzene


ans =

random thoughts

it is also an error access a non-existent key, so we can check if it exists like this.

if cM.isKey('tre')
    cM('tre')
else
    'no tre key found.'
end

ans =

no tre key found.

Summary

These are a few of the ways to store/organize data in matlab scripts/functions.

% categories: basic

Published with MATLAB® 7.12

Contents

Using cmu.units in Matlab for basic calculations

note you need to install the +cmu package for this to work.

clear all; clc; close all;

Load the units package

units is a new type of object in Matlab that stores the units, enforces proper unit algebra and works with most mathematical operations in Matlab. You load the units package into a variable; by convention: u the default set of base units are the SI units.

u = cmu.units;

Simple unit algebra

the basics of unit algebra are that like units can be added and subtracted. Unlike units can be multiplied and divided. when you assign a unit to a number, it is automatically converted into the base units.

5*u.kg % a mass
5*u.lb % another mass
6*u.m/u.s  % a velocity

1*u.m + 10*u.cm % this is ok, 1.1 m
% 1*u.m + 1*u.s  % this is not ok

5*kg
2.26796*kg
6*m/s
1.1*m

Temperature is a little special

most unit conversions are simple multiplications. Temperature conversions involve multiplication and an offset; e.g. F = C*9/5 + 32;

T = 298*u.K    % Kelvin is an absolute scale
Tf = 400*u.R   % Rankine is an absolute scale
T1 = u.degC(100) % this is 100 degC, and T1 is in Kelvin
T2 = u.degF(212) % this is 212 degF, and T2 is in Kelvin

% convert 32 degF to degC
u.degF2C(32)  %no units on the output
u.degC2F(100) %no units on the output

298*K
222.222*K
373.15*K
373.15*K

ans =

     0


ans =

   212

displaying units

a unit object has an "as" function that can display the unit in various forms

a = 1*u.kg;
a.as(u.lb)

% to do an actual conversion, you divide the unit by the units you want to
% convert to.
sprintf('%1.2f = %1.2f lb',a,a/u.lb)

ans =

2.205*lb


ans =

1.00 kg = 2.20 lb

Load the cmu.constants package

The gas constant, speed of light, etc... are stored in this package

clear all; u = cmu.units;
c = cmu.constants;
c.R  %the gas constant%% variations of the gas constant
c.R.as(u.J/u.mol/u.K)
c.R.as(u.J/(u.mol*u.K))
c.R.as(u.cal/u.mol/u.K)
c.R.as(u.dm^3*u.atm/u.mol/u.K)
c.R.as(u.BTU/u.lbmol/u.R)
c.R.as(u.ft^3*u.atm/(u.lbmol*u.R))

8.31447*m^2/s^2*kg/K/mol

ans =

8.314*J/mol/K


ans =

8.314*J/(mol*K)


ans =

1.986*cal/mol/K


ans =

0.082*dm^3*atm/mol/K


ans =

1.986*BTU/lbmol/R


ans =

0.730*ft^3*atm/(lbmol*R)

Arrays of units

t = [0 1 2 3 4]*u.s;
C = [5 3 1 0.5 0.05]*u.mol/u.L; % note these concentrations are stored
                                % internally as mol/m^3 because those are
                                % the base SI units

% we can change the units in a plot by converting them to the units we want
plot(t/u.min,C/(u.mol/u.L))
xlabel('Time (min)')
ylabel('Concentration (mol/L)')

units with Matlab functions

Many functions in Matlab such as ode45, ode15s, fzero, fsolve, min, max, etc... work with units. This works because we have overloaded these functions to work with units. Not all functions are overloaded though, so be careful! If you find you have lost the units, it means you used a function that was not overloaded. Please let us know about it!

functions that do not work with units

functions that require dimensionless arguments (e.g. trig functions, exp, log, etc...) will usually fail if you pass a unit in. You must divide the arguments by the appropriate units to make them dimensionless

a = 5*u.mol;
sin(a/u.mol)

ans =

   -0.9589

Alternative base units

you can specify 'SI', 'CGS' or 'American' as the base units SI/MKS: {'m','s','kg', 'K', 'mol','coul'} CGS: {'cm','s','gm','K', 'mol','coul'} American: {'in','s','lb','R', 'mol','coul'

u = cmu.units('American');
a = 2*u.ft
a.as(u.m)

% you can also specify which units are your base. Note the order of base
% units must be: length, time, mass, temperature, charge, mol
% and all of them must be specified.
u = cmu.unit.units('mm','min','ton','R','coul','mol');
a = u.cm
a.as(u.m)

24*in

ans =

0.610*m

10*mm

ans =

0.010*m

simplified units

there may be times when you need units conversion, but you only want simple numbers and not unit objects, e.g. because some Matlab function doesn't handle units. You can load the simple_units structure to get a set of conversion factors. Unit algebra is not used and units are kept track of, so you have to know what the units are.

u = cmu.unit.simple_units;
a = 1*u.kg
a/u.lb
a/u.min

% tags: units, +cmu

a =

    0.0011


ans =

    2.2046


ans =

    0.0011

Published with MATLAB® 7.10