Estimating the boiling point of water
January 01, 2012 at 07:40 PM | categories: uncategorized | View Comments
Contents
Estimating the boiling point of water
John Kitchin
I got distracted looking for Shomate parameters for ethane today, and came across this website on predicting the boiling point of water using the Shomate equations. The basic idea is to find the temperature where the Gibbs energy of water as a vapor is equal to the Gibbs energy of the liquid.
clear all; close all
Liquid water
http://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185&Units=SI&Mask=2#Thermo-Condensed valid over 298-500
Hf_liq = -285.830; % kJ/mol S_liq = 0.06995; % kJ/mol/K shomateL = [-203.6060 1523.290 -3196.413 2474.455 3.855326 -256.5478 -488.7163 -285.8304];
Gas phase water
http://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185&Units=SI&Mask=1&Type=JANAFG&Table=on#JANAFG
Interestingly, these parameters are listed as valid only above 500K. That means we have to extrapolate the values down to 298K. That is risky for polynomial models, as they can deviate substantially outside the region they were fitted to.
Hf_gas = -241.826; % kJ/mol S_gas = 0.188835; % kJ/mol/K shomateG = [30.09200 6.832514 6.793435 -2.534480 0.082139 -250.8810 223.3967 -241.8264];
Compute G over a range of temperatures.
T = linspace(0,200)' + 273.15; % temperature range from 0 to 200 degC t = T/1000; % normalize sTT by 1/1000 so entropies are in kJ/mol/K sTT = [log(t) t t.^2/2 t.^3/3 -1./(2*t.^2) 0*t.^0 t.^0 0*t.^0]/1000; hTT = [t t.^2/2 t.^3/3 t.^4/4 -1./t 1*t.^0 0*t.^0 -1*t.^0]; Gliq = Hf_liq + hTT*shomateL - T.*(sTT*shomateL); Ggas = Hf_gas + hTT*shomateG - T.*(sTT*shomateG);
Interpolate the difference between the two vectors to find the boiling point
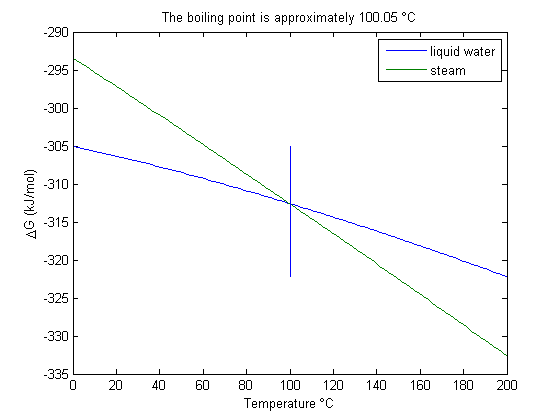
The boiling point is where Gliq = Ggas, so we solve Gliq(T)-Ggas(T)=0 to find the point where the two free energies are equal.
f = @(t) interp1(T,Gliq-Ggas,t); bp = fzero(f,373)
bp = 373.2045
Plot the two free energies
You can see the intersection occurs at approximately 100 degC.
plot(T-273.15,Gliq,T-273.15,Ggas) line([bp bp]-273.15,[min(Gliq) max(Gliq)]) legend('liquid water','steam') xlabel('Temperature \circC') ylabel('\DeltaG (kJ/mol)') title(sprintf('The boiling point is approximately %1.2f \\circC', bp-273.15))
Summary
The answer we get us 0.05 K too high, which is not bad considering we estimated it using parameters that were fitted to thermodynamic data and that had finite precision and extrapolated the steam properties below the region the parameters were stated to be valid for.
% tags: thermodynamics