Counting roots
September 10, 2011 at 11:06 PM | categories: odes, nonlinear algebra | View Comments
Counting roots
John Kitchin
Contents
Problem statement
The goal here is to determine how many roots there are in a nonlinear function we are interested in solving. For this example, we use a cubic polynomial because we know there are three roots.
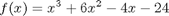
function main
clc; clear all; close all;
Use roots for this polynomial
This ony works for a polynomial, it does not work for any other nonlinear function.
roots([1 6 -4 -24])
ans =
-6.0000
2.0000
-2.0000
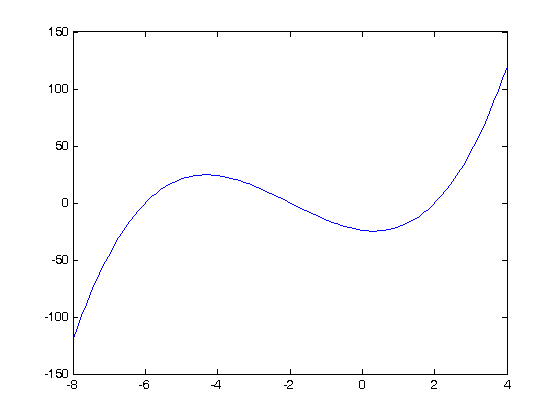
Plot the function to see where the roots are
x = linspace(-8,4); fx = x.^3 + 6*x.^2 - 4*x - 24; plot(x,fx)
method 1
count the number of times the sign changes in the interval. We determine the sign of each element (-1, 0 or +1) and then use a a loop to go through each element. A sign change is detected when an element is not equal to the previous element. Note this is not foolproof; we may over count roots if we get a sequence -1 0 1. We check for that by making sure neither of the two elements being compared are zero.
sign_fx = sign(fx); count = 0; for i=2:length(sign_fx) if sign_fx(i) ~= sign_fx(i-1) && sign_fx(i) ~= 0 && sign_fx(i-1) ~= 0 count = count + 1; disp(sprintf('A root is between x = %f and %f',x(i-1),x(i))) end end disp(sprintf('The number of sign changes is %i.',count))
A root is between x = -6.060606 and -5.939394 A root is between x = -2.060606 and -1.939394 A root is between x = 1.939394 and 2.060606 The number of sign changes is 3.
method 1a
this one line code also counts sign changes. the diff command makes all adjacent, identical elements equal zero, and sign changes = 2 (1 - (-1)) or (-1 - 1). Then we just sum up the diff vector, divide by two, and that is the number of roots. Note that no check for 0 is needed; you will get 1/2 a sign change from -1 to 0. and another half from 0 to 1. They add up to a whole sign change.
sum(abs(diff(sign_fx))/2)
ans =
3
Discussion
Method 1 is functional but requires some programming. Method 1a is concise but probably tricky to remember.
Method 2
using events in an ODE solver Matlab can identify events in the solution to an ODE, for example, when a function has a certain value, e.g. f(x) = 0. We can take advantage of this to find the roots and number of roots in this case.
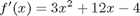
with f(-8) = -120
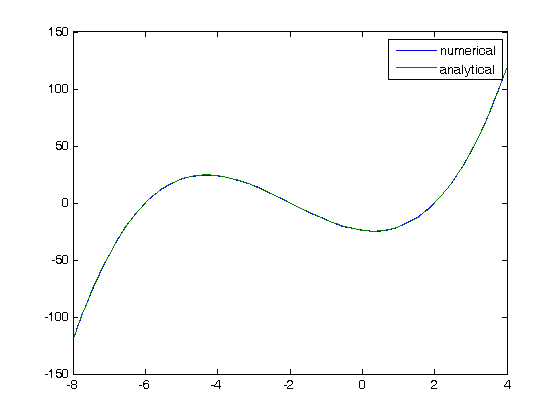
xspan = [-8 4]; fp0 = -120; options = odeset('Events',@event_function); [X,Y,XE,VE,IE] = ode45(@myode,xspan,fp0,options); XE % these are the x-values where the function equals zero nroots = length(XE); disp(sprintf('Found %i roots in the x interval',nroots)) % lets compare the solution to the original function to make sure they are % the same. figure plot(X,Y,x,fx) legend 'numerical' 'analytical'
function dfdx = myode(x,f) dfdx = 3*x^2 + 12*x - 4; function [value,isterminal,direction] = event_function(t,y) value = y - 0; % then value = 0, an event is triggered isterminal = 0; % do not terminate after the first event direction = 0; % get all the zeros % categories: ODEs, nonlinear algebra
XE =
-6.0000
-2.0000
2.0000
Found 3 roots in the x interval
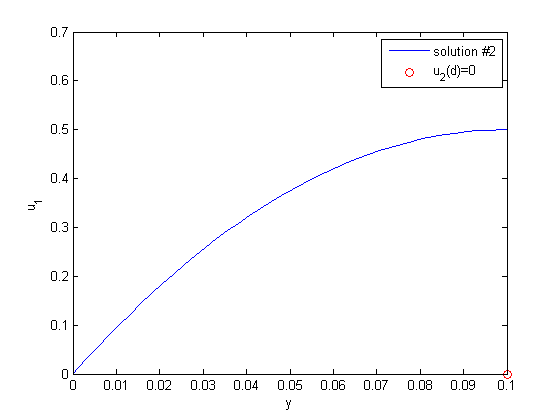
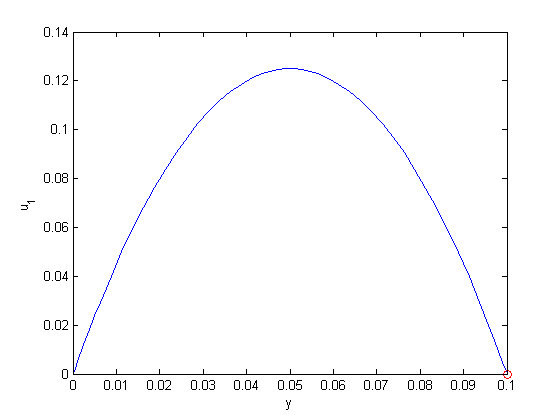
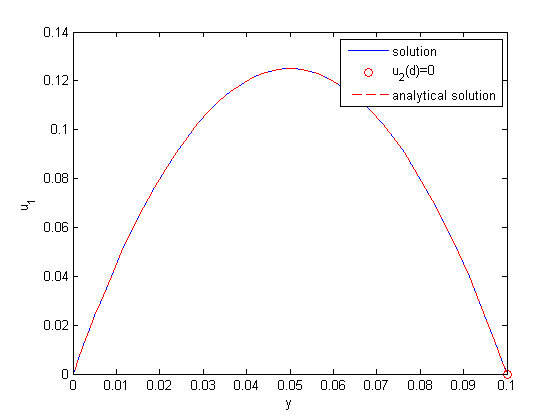
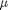 between two stationary plates separated by distance
between two stationary plates separated by distance 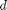 and driven by a pressure drop
and driven by a pressure drop 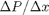 , the governing equations on the velocity
, the governing equations on the velocity  of the fluid are (assuming flow in the x-direction with the velocity varying only in the y-direction):
of the fluid are (assuming flow in the x-direction with the velocity varying only in the y-direction):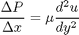
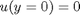 and
and 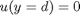 , i.e. the no-slip condition at the edges of the plate.
, i.e. the no-slip condition at the edges of the plate.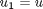 ,
, 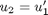 and then
and then 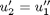 . This leads to:
. This leads to: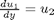
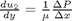
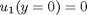 and
and 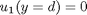 .
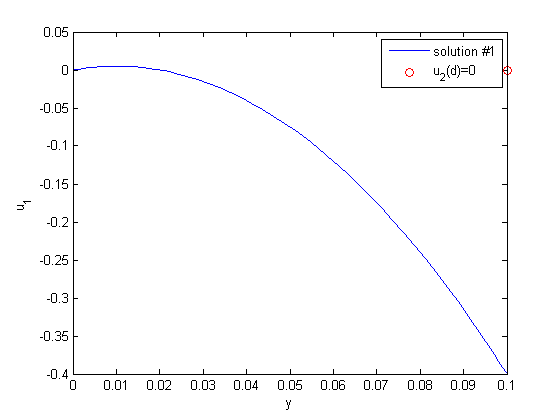
.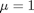 , and
, and  .
.
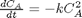 with the initial condition
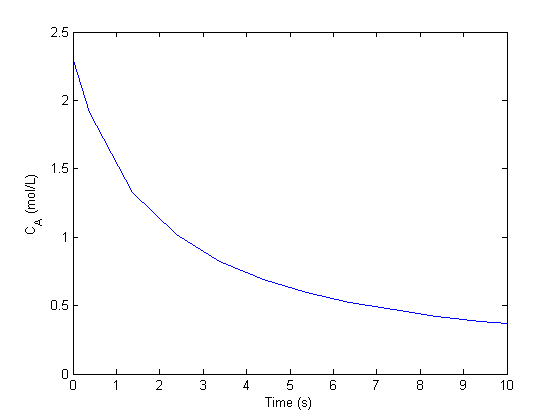
with the initial condition 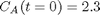 mol/L and
mol/L and 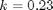 L/mol/s, compute the time it takes for
L/mol/s, compute the time it takes for 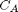 to be reduced to 1 mol/L.
to be reduced to 1 mol/L.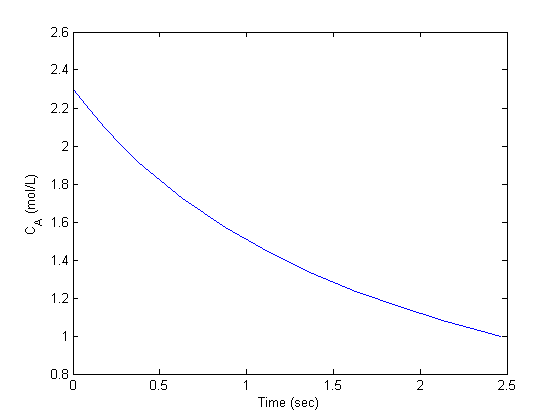
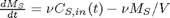 with the initial condition that
with the initial condition that  . The wrinkle is that
. The wrinkle is that
 You can see the discontinuity in the salt concentration at 10 minutes due to the discontinous change in the entering salt concentration.
You can see the discontinuity in the salt concentration at 10 minutes due to the discontinous change in the entering salt concentration.
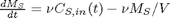
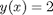 . In a numerical solution to an ODE we get a vector of independent variable values, and the corresponding function values at those values. To solve for a particular function value we need a different approach. This post will show one way to do that in Matlab.
. In a numerical solution to an ODE we get a vector of independent variable values, and the corresponding function values at those values. To solve for a particular function value we need a different approach. This post will show one way to do that in Matlab.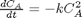 with the initial condition
with the initial condition 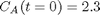 mol/L and
mol/L and 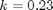 L/mol/s, compute the time it takes for
L/mol/s, compute the time it takes for 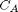 to be reduced to 1 mol/L.
to be reduced to 1 mol/L.