Numerically calculating an effectiveness factor for a porous catalyst bead
November 18, 2011 at 04:25 PM | categories: bvp | View Comments
Contents
Numerically calculating an effectiveness factor for a porous catalyst bead
John Kitchin
If reaction rates are fast compared to diffusion in a porous catalyst pellet, then the observed kinetics will appear to be slower than they really are because not all of the catalyst surface area will be effectively used. For example, the reactants may all be consumed in the near surface area of a catalyst bead, and the inside of the bead will be unutilized because no reactants can get in due to the high reaction rates.
References: Ch 12. Elements of Chemical Reaction Engineering, Fogler, 4th edition.
function main
close all; clc; clear all
The governing equations for reaction and diffusion
A mole balance on the particle volume in spherical coordinates with a first order reaction leads to: 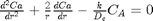 with boundary conditions
with boundary conditions 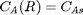 and
and 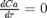 at
at 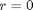 . We convert this equation to a system of first order ODEs by letting
. We convert this equation to a system of first order ODEs by letting 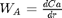 .
.
function dYdt = ode(r,Y) Wa = Y(1); % molar rate of delivery of A to surface of particle Ca = Y(2); % concentration of A in the particle at r if r == 0 dWadr = 0; % this solves the singularity at r = 0 else dWadr = -2*Wa/r + k/De*Ca; end dCadr = Wa; dYdt = [dWadr; dCadr]; end
Parameters for this problem
De = 0.1; % diffusivity cm^2/s R = 0.5; % particle radius, cm k = 6.4; % rate constant (1/s) CAs = 0.2; % concentration of A at outer radius of particle (mol/L)
Solving the BVP
we have a condition of no flux at r=0 and Ca® = CAs, which makes this a boundary value problem. We use the shooting method here, and guess what Ca(0) is and iterate the guess to get Ca® = CAs.
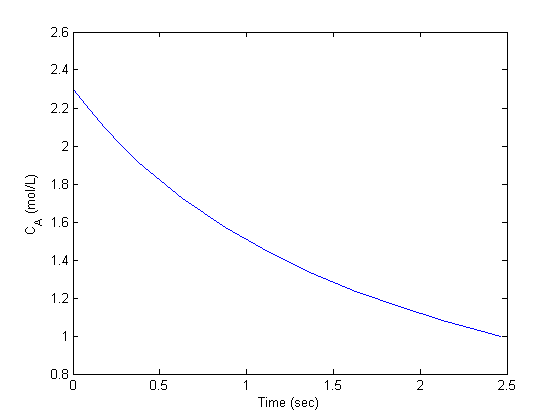
Ca0 = 0.029315; % Ca(0) (mol/L) guessed to satisfy Ca(R) = CAs Wa0 = 0; % no flux at r=0 (mol/m^2/s) init = [Wa0 Ca0]; rspan = [0 R]; [r Y] = ode45(@ode,rspan, init); Ca = Y(:,2); plot(r,Ca) xlabel('Particle radius') ylabel('C_A')
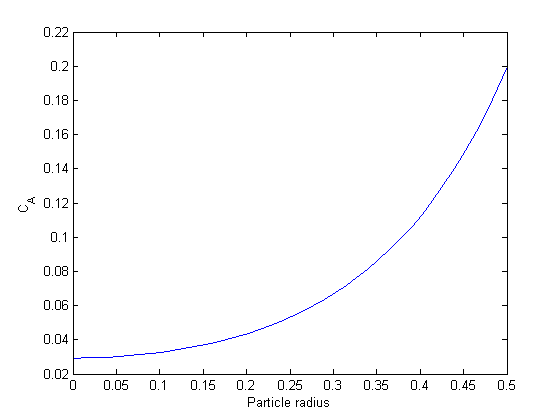
You can see the concentration of A inside the particle is significantly lower than outside the particle. That is because it is reacting away faster than it can diffuse into the particle. Hence, the overall reaction rate in the particle is lower than it would be without the diffusion limit.
Compute the effectiveness factor numerically
The effectiveness factor is the ratio of the actual reaction rate in the particle with diffusion limitation to the ideal rate in the particle if there was no concentration gradient:
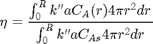
We will evaluate this numerically from our solution.
eta_numerical = trapz(r, k*Ca*4*pi.*(r.^2))/trapz(r, k*CAs*4*pi.*(r.^2))
eta_numerical =
0.5635
Analytical solution for a first order reaction
an analytical solution exists for this problem.
phi = R*sqrt(k/De); eta = (3/phi^2)*(phi*coth(phi)-1)
eta =
0.5630
Why go through the numerical solution when an analytical solution exists? The analytical solution here is only good for 1st order kinetics in a sphere. What would you do for a complicated rate law? You might be able to find some limiting conditions where the analytical equation above is relevant, and if you are lucky, they are appropriate for your problem. If not, it's a good thing you can figure this out numerically!
end % categories: BVP % tags: reaction engineering


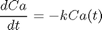
 is a parameter, and we want to solve the equation for a couple of values of
is a parameter, and we want to solve the equation for a couple of values of 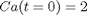 , how long does it take to get
, how long does it take to get 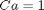 , and how sensitive is the answer to small variations in
, and how sensitive is the answer to small variations in 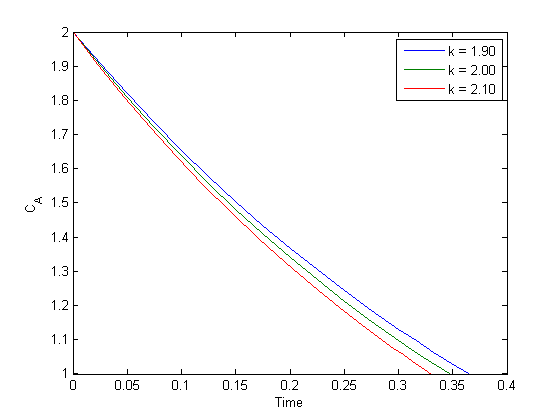
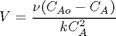
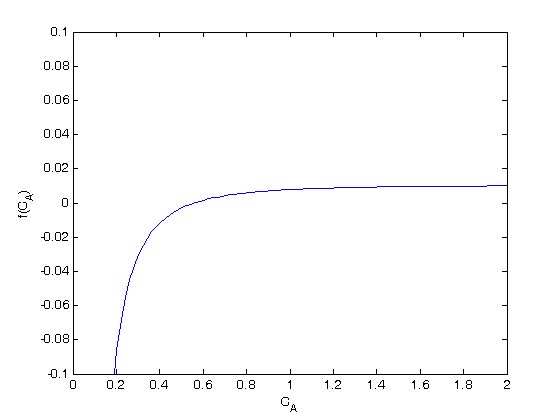
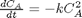 with the initial condition
with the initial condition 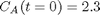 mol/L and
mol/L and 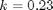 L/mol/s, compute the time it takes for
L/mol/s, compute the time it takes for 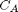 to be reduced to 1 mol/L.
to be reduced to 1 mol/L.