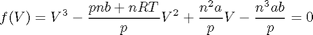Determining linear independence of a set of vectors
Occasionally we have a set of vectors and we need to determine whether the vectors are linearly independent of each other. This may be necessary to determine if the vectors form a basis, or to determine how many independent equations there are, or to determine how many independent reactions there are.
Reference: Kreysig, Advanced Engineering Mathematics, sec. 7.4
Contents
Problem set 7.4 - #15
v1 = [6 0 3 1 4 2];
v2 = [0 -1 2 7 0 5];
v3 = [12 3 0 -19 8 -11];
R = rank([v1; v2; v3])
[rows, ~] = size([v1; v2; v3])
R =
2
rows =
3
x = [v1.' v2.']\v3.'
x(1)*v1 + x(2)*v2
v3
x =
2.0000
-3.0000
ans =
12.0000 3.0000 0.0000 -19.0000 8.0000 -11.0000
v3 =
12 3 0 -19 8 -11
Problem set 7.4 #17
v1 = [0.2 1.2 5.3 2.8 1.6];
v2 = [4.3 3.4 0.9 2.0 -4.3];
rank([v1; v2])
ans =
2
Near deficient rank
the rank command roughly works in the following way: the matrix is converted to a reduced row echelon form, and then the number of rows that are not all equal to zero are counted. Matlab uses a tolerance to determine what is equal to zero. If there is uncertainty in the numbers, you may have to define what zero is, e.g. if the absolute value of a number is less than 1e-5, you may consider that close enough to be zero. The default tolerance is usually very small, of order 1e-15.
A = [[1 2 3];
[0 2 3];
[0 0 1e-6]];
rank(A)
ans =
3
rank with tolerance
If we believe that any number less than 1e-5 is practically equivalent to zero, we can use that information to compute the rank like this.
tolerance = 1e-5;
rank(A,tolerance)
ans =
2
Application to independent chemical reactions.
reference: Exercise 2.4 in Chemical Reactor Analysis and Design Fundamentals by Rawlings and Ekerdt.
The following reactions are proposed in the hydrogenation of bromine:
Let this be our species vector: v = [H2 H Br2 Br HBr]^T
the reactions are then defined by M*v where M is a stoichometric matrix in which each row represents a reaction with negative stoichiometric coefficients for reactants, and positive stoichiometric coefficients for products. A stoichiometric coefficient of 0 is used for species not participating in the reaction.
M = [[-1 0 -1 0 2];
[ 0 0 -1 2 0];
[-1 1 0 -1 1];
[ 0 -1 -1 1 1];
[ 1 -1 0 1 -1];
[ 0 0 1 -2 0]];
rank(M)
ans =
3
choosing independent reactions
We can identify independent reactions by examining the reduced row echelon form of the matrix where the reactions are in the columns rather than rows. That is simply the transpose of the M matrix above. The columns with leading ones correspond to the reactions that can form a basis, i.e. the independent reactions.
rref(M')
ans =
1 0 0 1 0 0
0 1 0 0 0 -1
0 0 1 -1 -1 0
0 0 0 0 0 0
0 0 0 0 0 0
basis = transpose(M(1:3,:));
reaction_4 = M(4,:).';
reaction_5 = M(5,:).';
reaction_6 = M(6,:).';
x_4 = basis\reaction_4
x_5 = basis\reaction_5
x_6 = basis\reaction_6
x_4 =
1.0000
0.0000
-1.0000
x_5 =
-0.0000
0.0000
-1.0000
x_6 =
-0.0000
-1.0000
0.0000
lets also demonstrate that reaction 1 is not a linear combination of reactions 2 and 3.
reaction_1 = M(1,:).';
x_1 = basis\reaction_1
x_1 =
1.0000
0.0000
0.0000
Related posts
transposition rules
solving linear equations
 . Let's plot that on the same graph. We will use a dashed red line
. Let's plot that on the same graph. We will use a dashed red line

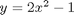
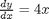
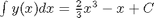
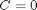 .
.