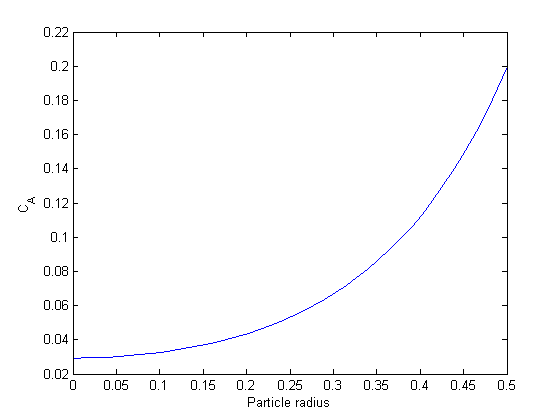
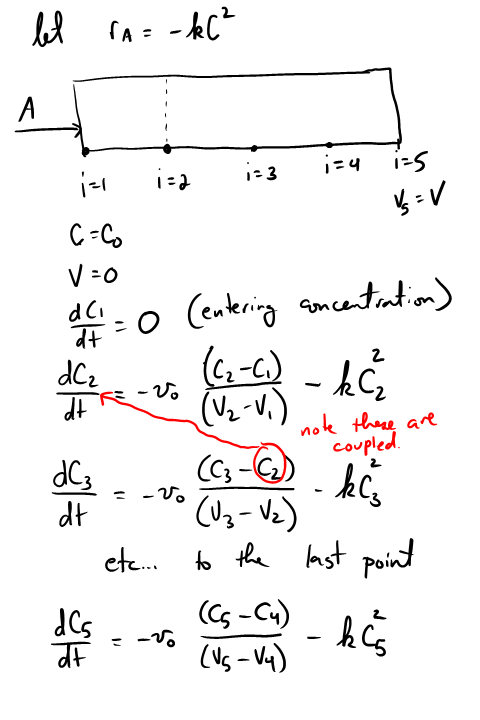
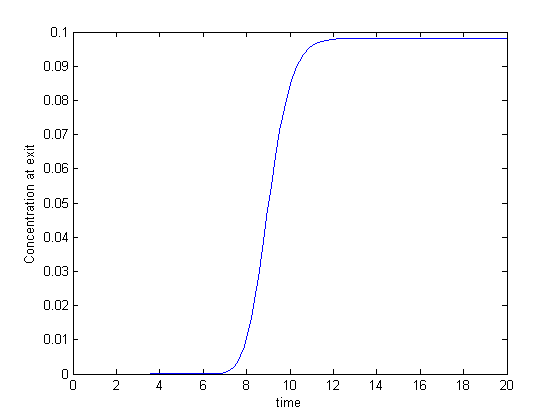
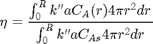3D plots of the steam tables
November 23, 2011 at 02:02 AM | categories: plotting | View Comments
Contents
3D plots of the steam tables
John Kitchin
For fun let's make some 3D plots of the steam tables. We will use the XSteam module to map out the pressure, entropy and temperature of steam, and plot the 3D mapping.
clear all; close all; clc
create vectors that we will calculate T for
P = logspace(-2,3); %bar
S = linspace(0,10);
create meshgrid
these are matrices that map out a plane of P,S space
[xdata,ydata] = meshgrid(P,S); zdata = zeros(size(xdata));
calculate T for each (p,S) pair in the meshgrids
zdata = arrayfun(@(p,s) XSteam('T_ps',p,s),xdata,ydata);
create the 3D plot
we use a lighted surface plot here
surfl(xdata,ydata,zdata) xlabel('P (bar)') ylabel('S (kJ/kg/K)') zlabel('T (K)') zlim([0 400])
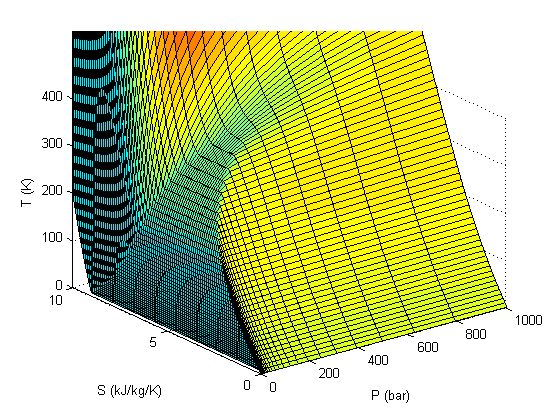
customize the look of the surface plot
this smooths the faces out
shading interp
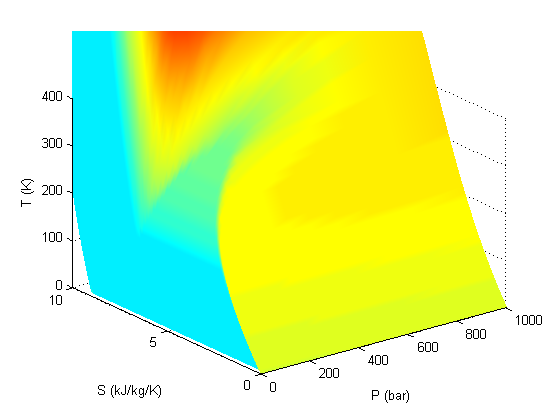
colormap pink
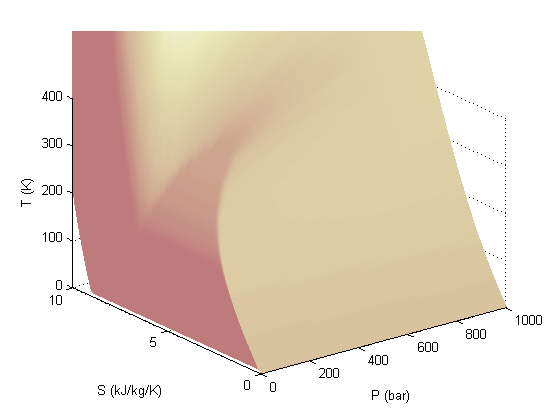
Add the saturated vapor and liquid lines, and the critical point
hold all Tsat = arrayfun(@(p) XSteam('Tsat_p',p),P); sV = arrayfun(@(p) XSteam('sV_p',p),P); sL = arrayfun(@(p) XSteam('sL_p',p),P); plot3(P,sV,Tsat,'r-','linewidth',5) plot3(P,sL,Tsat,'g-','linewidth',5) tc = 373.946; % C pc = 220.584525; % bar sc =XSteam('sV_p',pc); plot3(pc,sc,tc,'ro','markerfacecolor','b') % the critical point legend '' 'sat. vapor' 'sat. liquid' 'critical point'
Warning: Legend not supported for patches with FaceColor 'interp'
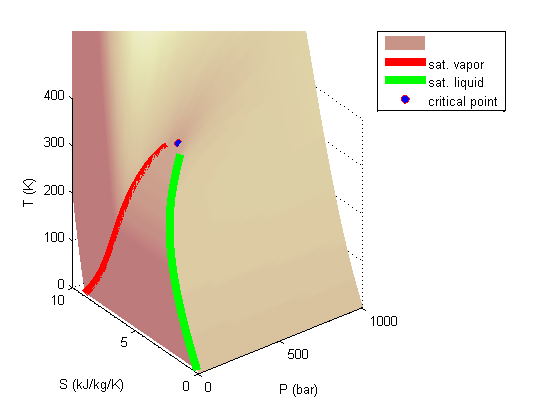
Summary
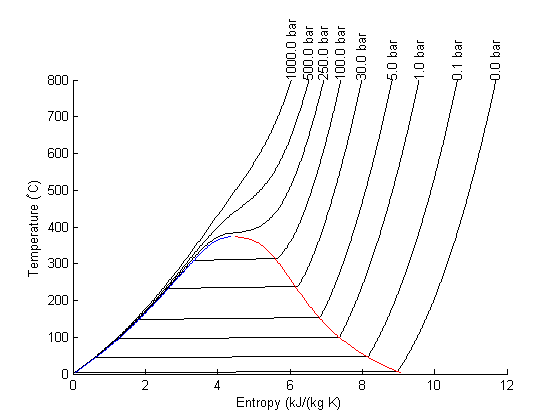
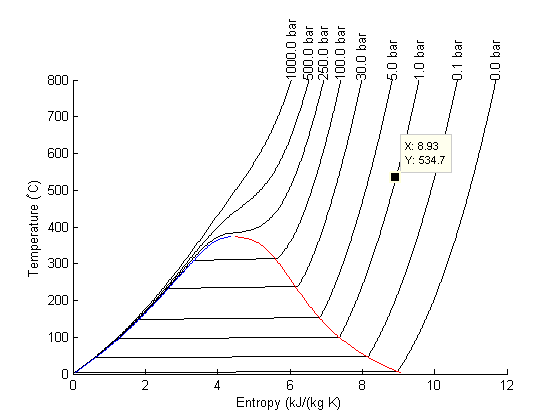
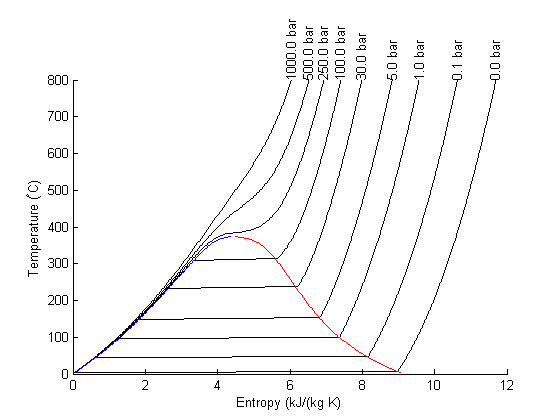
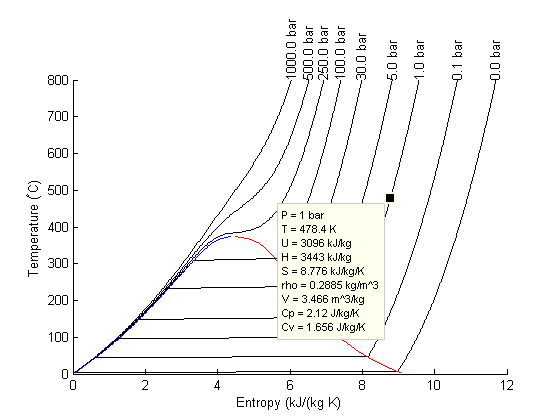
There are lots of options in making 3D plots. They look nice, and from the right perspective can help see how different properties are related. Compare this graph to the one in Post 1484 , where isobars had to be plotted in the 2d graph.
% categories: plotting % tags: thermodynamics
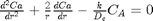 with boundary conditions
with boundary conditions 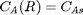 and
and 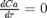 at
at 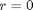 . We convert this equation to a system of first order ODEs by letting
. We convert this equation to a system of first order ODEs by letting 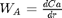 .
.