Finding equilibrium composition by direct minimization of Gibbs free energy on mole numbers
December 25, 2011 at 07:59 PM | categories: optimization | View Comments
Finding equilibrium composition by direct minimization of Gibbs free energy on mole numbers
John Kitchin
Adapted from problem 4.5 in Cutlip and Shacham
Contents
- Problem setup
- The Gibbs energy of a mixture
- Linear equality constraints for atomic mass conservation
- Bounds on mole numbers
- initial guess for the solver
- Setup minimization
- Verify the equality constraints were met
- Results
- Water gas shift equilibrium
- WGS equilibrium constant at 1000K
- Equilibrium constant based on mole numbers
- Summary
Problem setup
Ethane and steam are fed to a steam cracker at a total pressure of 1 atm and at 1000K at a ratio of 4 mol H2O to 1 mol ethane. Estimate the equilibrium distribution of products (CH4, C2H4, C2H2, CO2, CO, O2, H2, H2O, and C2H6).
Solution method: We will construct a Gibbs energy function for the mixture, and obtain the equilibrium composition by minimization of the function subject to elemental mass balance constraints.
function main
R = 0.00198588; % kcal/mol/K T = 1000; % K % we store the species names in a cell array since they have different % lengths (i.e. different number of characters in names). species = {'CH4' 'C2H4' 'C2H2' 'CO2' 'CO' 'O2' 'H2' 'H2O' 'C2H6'}; % % $G_^\circ for each species. These are the heats of formation for each % species. Gjo = [4.61 28.249 40.604 -94.61 -47.942 0 0 -46.03 26.13]; % kcal/mol
The Gibbs energy of a mixture
We start with 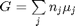 . Recalling that we define
. Recalling that we define 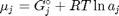 , and in the ideal gas limit,
, and in the ideal gas limit, 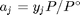 , and that
, and that 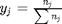 . Since in this problem, P = 1 atm, this leads to the function
. Since in this problem, P = 1 atm, this leads to the function 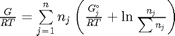 .
.
function G = func(nj) Enj = sum(nj); G = sum(nj.*(Gjo/R/T + log(nj/Enj))); end
Linear equality constraints for atomic mass conservation
The total number of each type of atom must be the same as what entered the reactor. These form equality constraints on the equilibrium composition. We express these constraints as: 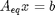 where
where  is a vector of the moles of each species present in the mixture. CH4 C2H4 C2H2 CO2 CO O2 H2 H2O C2H6
is a vector of the moles of each species present in the mixture. CH4 C2H4 C2H2 CO2 CO O2 H2 H2O C2H6
Aeq = [0 0 0 2 1 2 0 1 0 % oxygen balance 4 4 2 0 0 0 2 2 6 % hydrogen balance 1 2 2 1 1 0 0 0 2]; % carbon balance % the incoming feed was 4 mol H2O and 1 mol ethane beq = [4 % moles of oxygen atoms coming in 14 % moles of hydrogen atoms coming in 2]; % moles of carbon atoms coming in
Bounds on mole numbers
No mole number can be negative, so we define a lower bound of zero for each mole number. In principle there are upper bounds too, but it is unecessary to define them here.
LB = [0 0 0 0 0 0 0 0 0]; % no mole numbers less than zero
initial guess for the solver
these are the guesses suggested in the book.
x0 = [1e-3 1e-3 1e-3 0.993 1 1e-4 5.992 1 1e-3]; % initial guess
Setup minimization
fmincon does not solve this problem with the default solver, and warns you to pick another one, either 'interior-point' or 'sqp'. Both work for this problem.
options = optimset('Algorithm','sqp'); [x fval] = fmincon(@func,x0,[],[],Aeq,beq,LB,[],[],options); for i=1:numel(x) fprintf('%5d%10s%10.3g\n',i,species{i},x(i)) end
Local minimum possible. Constraints satisfied.
fmincon stopped because the size of the current step is less than
the default value of the step size tolerance and constraints are
satisfied to within the default value of the constraint tolerance.
1 CH4 0.0664
2 C2H4 8.88e-008
3 C2H2 2.76e-021
4 CO2 0.545
5 CO 1.39
6 O2 4.56e-021
7 H2 5.35
8 H2O 1.52
9 C2H6 1.6e-007
Verify the equality constraints were met
you can see here the constraints were met.
Aeq*x' beq
ans =
4
14
2
beq =
4
14
2
Results
Interestingly there is a distribution of products! That is interesting because only steam and ethane enter the reactor, but a small fraction of methane is formed! The main product is hydrogen. The stoichiometry of steam reforming is ideally  . Even though nearly all the ethane is consumed, we don't get the full yield of hydrogen. It appears that another equilibrium, one between CO, CO2, H2O and H2, may be limiting that, since the rest of the hydrogen is largely in the water. It is also of great importance that we have not said anything about reactions, i.e. how these products were formed. This is in stark contrast to Post 1589 where stoichiometric coefficients were necessary to perform the minimization.
. Even though nearly all the ethane is consumed, we don't get the full yield of hydrogen. It appears that another equilibrium, one between CO, CO2, H2O and H2, may be limiting that, since the rest of the hydrogen is largely in the water. It is also of great importance that we have not said anything about reactions, i.e. how these products were formed. This is in stark contrast to Post 1589 where stoichiometric coefficients were necessary to perform the minimization.
Water gas shift equilibrium
The water gas shift reaction is: 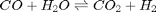 . We can compute the Gibbs free energy of the reaction from the heats of formation of each species. Assuming these are the formation energies at 1000K, this is the reaction free energy at 1000K.
. We can compute the Gibbs free energy of the reaction from the heats of formation of each species. Assuming these are the formation energies at 1000K, this is the reaction free energy at 1000K.
G_wgs = Gjo(4) + Gjo(7) - Gjo(5) - Gjo(8)
G_wgs = -0.6380
WGS equilibrium constant at 1000K
exp(-G_wgs/R/T)
ans =
1.3789
Equilibrium constant based on mole numbers
One normally uses activities to define the equilibrium constant. Since there are the same number of moles on each side of the reaction all factors that convert mole numbers to activity, concentration or pressure cancel, so we simply consider the ratio of mole numbers here.
x(4)*x(7)/(x(5)*x(8))
ans =
1.3789
Clearly, there is an equilibrium between these species that prevents the complete reaction of steam reforming.
Summary
This is an appealing way to minimize the Gibbs energy of a mixture. No assumptions about reactions are necessary, and the constraints are easy to identify. The Gibbs energy function is especially easy to code.
end % categories: optimization % tags: Thermodynamics, reaction engineering % post_id = 1630; %delete this line to force new post; % permaLink = http://matlab.cheme.cmu.edu/2011/12/25/finding-equilibrium-composition-by-direct-minimization-of-gibbs-free-energy-on-mole-numbers/;
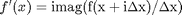 where the function
where the function 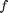 is evaluated in imaginary space with a small
is evaluated in imaginary space with a small 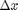 in the complex plane. The derivative is miraculously equal to the imaginary part of the result in the limit of
in the complex plane. The derivative is miraculously equal to the imaginary part of the result in the limit of  !
!
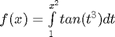 , and we now want to compute df/dx. Of course, this can be done
, and we now want to compute df/dx. Of course, this can be done 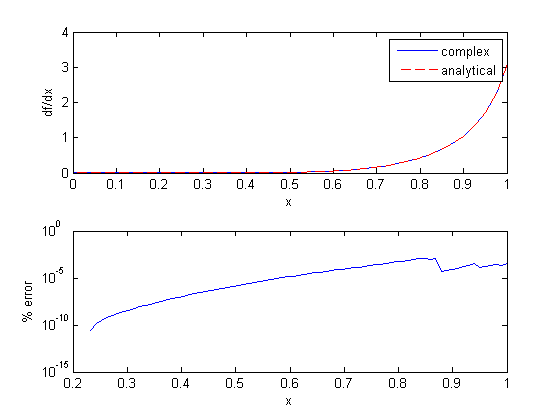
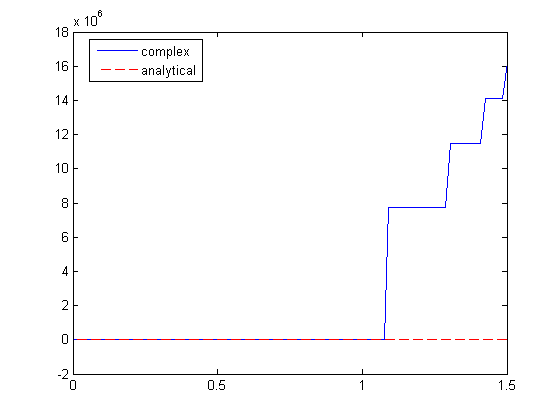
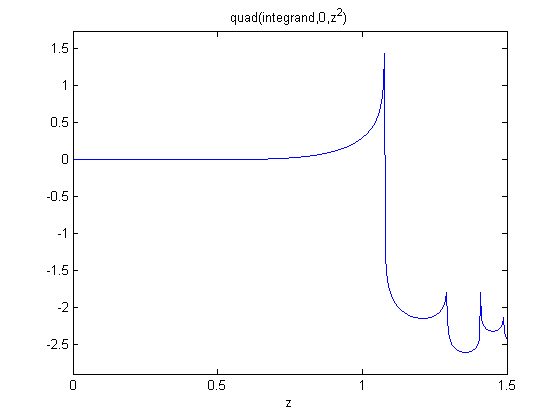
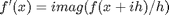 to approximate a derivative is one of the most interesting math facts I can't believe I didn't know before this post!
to approximate a derivative is one of the most interesting math facts I can't believe I didn't know before this post!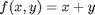 subject to the constraint that
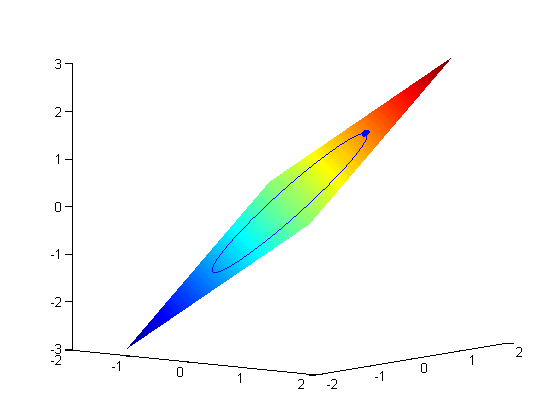
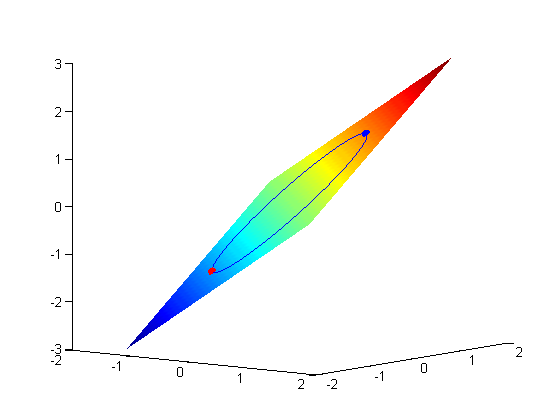
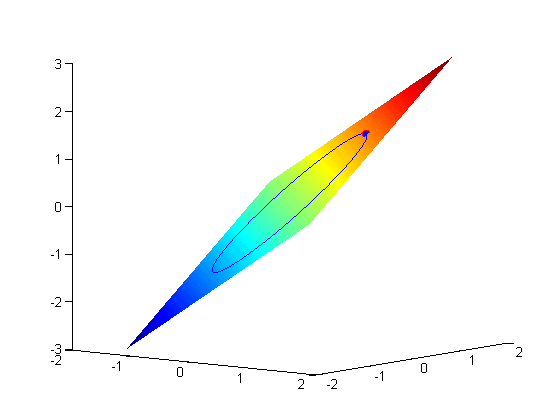
subject to the constraint that 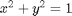 . The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. In
. The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. In 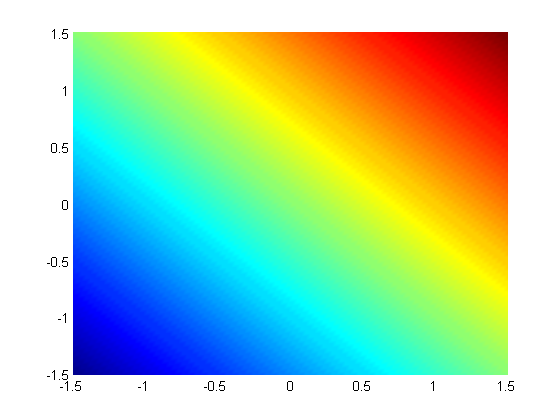
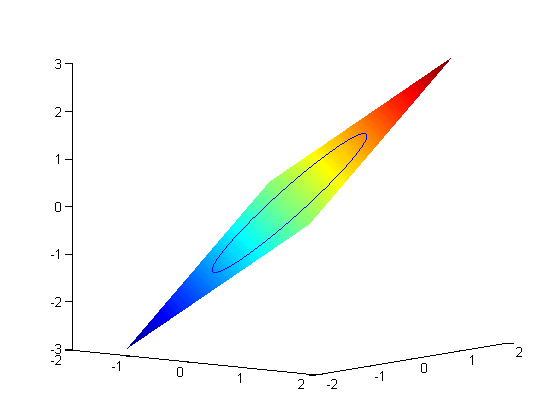
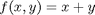 subject to the constraint that
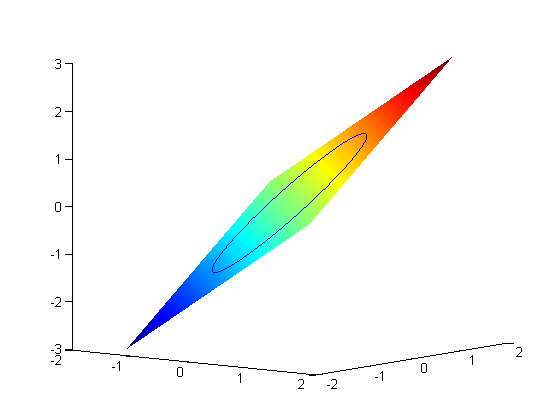
subject to the constraint that 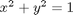 . The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. We plot these two functions here.
. The function we seek to maximize is an unbounded plane, while the constraint is a unit circle. We plot these two functions here.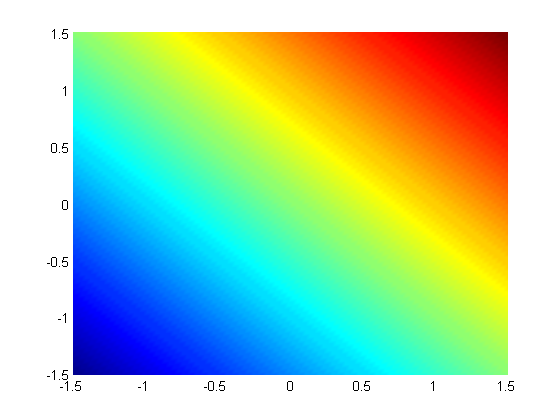
 where
where  , which is the constraint function. Since
, which is the constraint function. Since 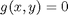 , we aren't really changing the original function, provided that the constraint is met!
, we aren't really changing the original function, provided that the constraint is met!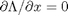 ,
, 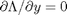 , and
, and 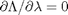 . the process for solving this is usually to analytically evaluate the partial derivatives, and then solve the unconstrained resulting equations, which may be nonlinear.
. the process for solving this is usually to analytically evaluate the partial derivatives, and then solve the unconstrained resulting equations, which may be nonlinear.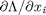 .
.
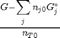
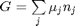 where
where 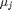 is the chemical potential of species
is the chemical potential of species  , and it is temperature and pressure dependent, and
, and it is temperature and pressure dependent, and 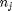 is the number of moles of species
is the number of moles of species 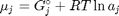 , where
, where 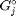 is the Gibbs energy in a standard state, and
is the Gibbs energy in a standard state, and  is the activity of species
is the activity of species  and stoichiometric coefficients:
and stoichiometric coefficients: 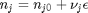 . Note that the reaction extent has units of moles.
. Note that the reaction extent has units of moles.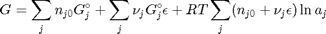
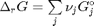 . With these observations we rewrite the equation as:
. With these observations we rewrite the equation as: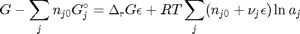
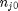 . It is desirable to avoid this, so we now rescale the equation by the total initial moles present,
. It is desirable to avoid this, so we now rescale the equation by the total initial moles present, 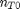 and define a new variable
and define a new variable 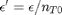 , which is dimensionless. This leads to:
, which is dimensionless. This leads to: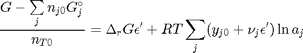
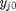 is the initial mole fraction of species
is the initial mole fraction of species 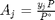 , where the numerator is the partial pressure of species
, where the numerator is the partial pressure of species 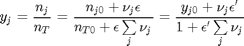
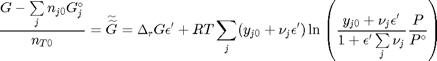
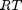 . This additional scaling makes the quantities dimensionless, and makes the quantity have a magnitude of order unity, but otherwise has no effect on the shape of the graph.
. This additional scaling makes the quantities dimensionless, and makes the quantity have a magnitude of order unity, but otherwise has no effect on the shape of the graph.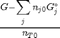
 can be. Recall that
can be. Recall that 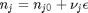 , and that
, and that 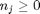 . Thus,
. Thus, 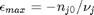 , and the maximum value that
, and the maximum value that 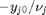 where
where 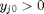 . When there are multiple species, you need the smallest
. When there are multiple species, you need the smallest 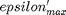 to avoid getting negative mole numbers.
to avoid getting negative mole numbers.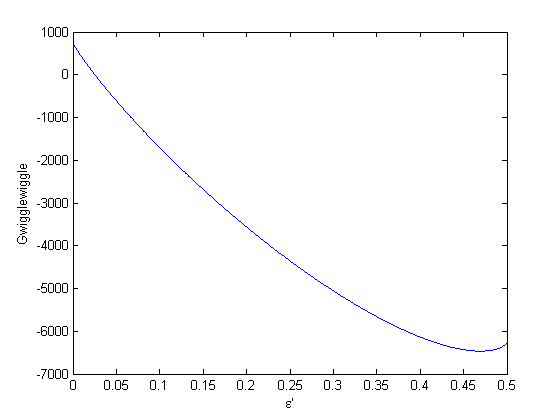
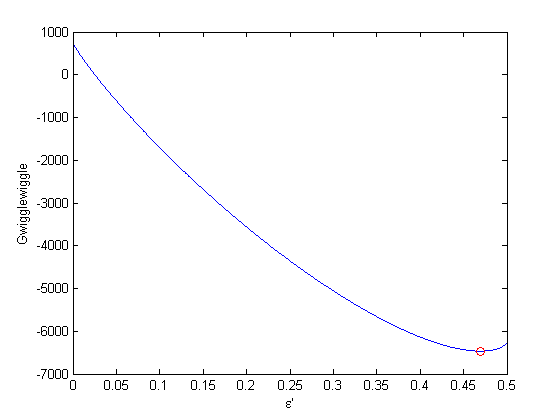
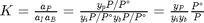 .
.