Model selection
October 01, 2011 at 11:52 PM | categories: data analysis | View Comments
Model selection
adapted from http://www.itl.nist.gov/div898/handbook/pmd/section4/pmd44.htm
In this example, we show some ways to choose which of several models fit data the best. We have data for the total pressure and temperature of a fixed amount of a gas in a tank that was measured over the course of several days. We want to select a model that relates the pressure to the gas temperature.
The data is stored in a text file download PT.txt , with the following structure
Contents
Run Ambient Fitted Order Day Temperature Temperature Pressure Value Residual 1 1 23.820 54.749 225.066 222.920 2.146
We need to read the data in, and perform a regression analysis on columns 4 and 5.
clc; clear all; close all
Read in the data
all the data is numeric, so we read it all into one matrix, then extract out the relevant columns
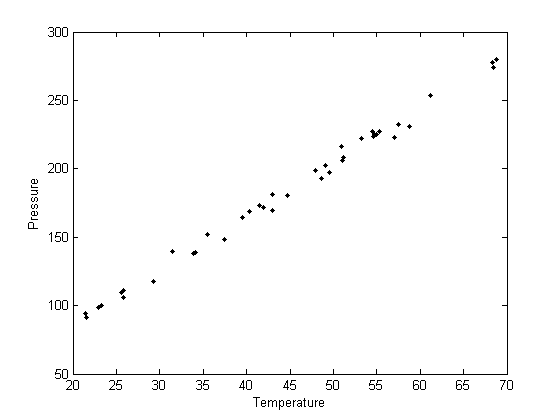
data = textread('PT.txt','','headerlines',2); run_order = data(:,1); run_day = data(:,2); ambientT = data(:,3); T = data(:,4); P = data(:,5); plot(T,P,'k. ') xlabel('Temperature') ylabel('Pressure')
Fit a line to the data for P(T) = a + bT
It appears the data is roughly linear, and we know from the ideal gas law that PV = nRT, or P = nR/V*T, which says P should be linearly correlated with V. Note that the temperature data is in degC, not in K, so it is not expected that P=0 at T = 0. let X = T, and Y = P for the regress syntax. The regress command expects a column of ones for the constant term so that the statistical tests it performs are valid. We get that column by raising the independent variable to the zero power.
X = [T.^0 T]; % [1 T1] Y = P; alpha = 0.05; % specifies the 95% confidence interval [b bint] = regress(Y,X,alpha)
b =
7.7490
3.9301
bint =
2.9839 12.5141
3.8275 4.0328
Note that the intercept is not zero, although, the confidence interval is fairly large, it does not include zero at the 95% confidence level.
Calculate R^2 for the line
The R^2 value accounts roughly for the fraction of variation in the data that can be described by the model. Hence, a value close to one means nearly all the variations are described by the model, except for random variations.
ybar = mean(Y);
SStot = sum((Y - ybar).^2);
SSerr = sum((Y - X*b).^2);
R2 = 1 - SSerr/SStot;
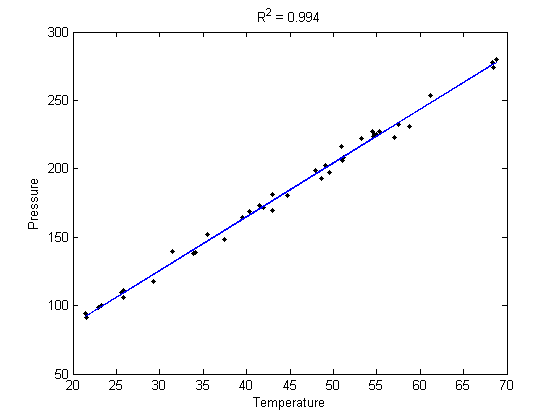
sprintf('R^2 = %1.3f',R2)
ans = R^2 = 0.994
Plot the data and the fit
plot(T,P,'k. ',T,X*b,'b -') xlabel('Temperature') ylabel('Pressure') title(sprintf('R^2 = %1.3f',R2))
Evaluating the model
The fit looks good, and R^2 is near one, but is it a good model? There are a few ways to examine this. We want to make sure that there are no systematic trends in the errors between the fit and the data, and we want to make sure there are not hidden correlations with other variables.
Plot the residuals
the residuals are the error between the fit and the data. The residuals should not show any patterns when plotted against any variables, and they do not in this case.
residuals = P - X*b; figure hold all subplot(1,3,1) plot(T,residuals,'ko') xlabel('Temperature') subplot(1,3,2) plot(run_order,residuals,'ko ') xlabel('run order') subplot(1,3,3) plot(ambientT,residuals,'ko') xlabel('ambient temperature')
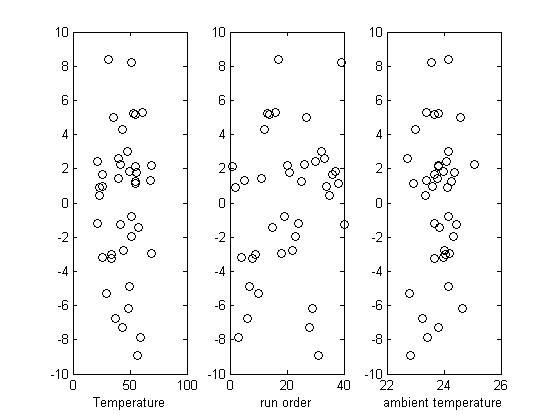
check for correlations between residuals
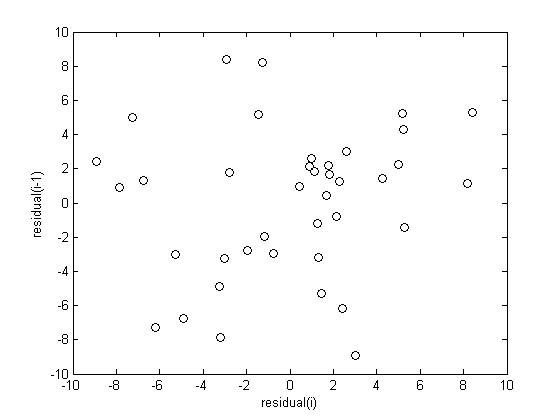
We assume all the errors are uncorrelated with each other. We use a lag plot, where we plot residual(i) vs residual(i-1), i.e. we look for correlations between adjacent residuals. This plot should look random, with no correlations if the model is good.
figure plot(residuals(2:end),residuals(1:end-1),'ko') xlabel('residual(i)') ylabel('residual(i-1)')
Alternative models
Lets consider a quadratic model instead.
X = [T.^0 T.^1 T.^2];
Y = P;
alpha = 0.05; % 95% confidence interval
[b bint] = regress(Y,X,alpha)
b =
9.0035
3.8667
0.0007
bint =
-4.7995 22.8066
3.2046 4.5288
-0.0068 0.0082
You can see that the 95% confidence interval on the constant and 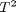 includes zero, so adding a parameter does not increase the goodness of fit. This is an example of overfitting the data, but it also makes you question whether the constant is meaningful in the linear model. The regress function expects a constant in the model, and the documentation says leaving it out
includes zero, so adding a parameter does not increase the goodness of fit. This is an example of overfitting the data, but it also makes you question whether the constant is meaningful in the linear model. The regress function expects a constant in the model, and the documentation says leaving it out
Alternative models
Lets consider a model with intercept = 0, P = alpha*T
X = [T]; Y = P; alpha = 0.05; % 95% confidence interval [b bint] = regress(Y,X,alpha) plot(T,P,'k. ',T,X*b,'b- ') xlabel('Temperature') ylabel('Pressure') legend 'data' 'fit' ybar = mean(Y); SStot = sum((Y - ybar).^2); SSerr = sum((Y - X*b).^2); R2 = 1 - SSerr/SStot; title(sprintf('R^2 = %1.3f',R2))
b =
4.0899
bint =
4.0568 4.1231
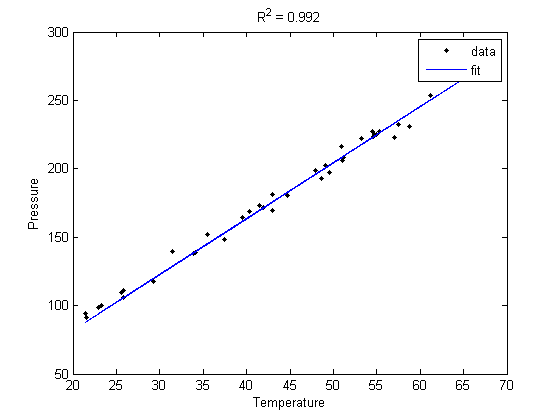
The fit is visually still good. and the R^2 value is only slightly worse.
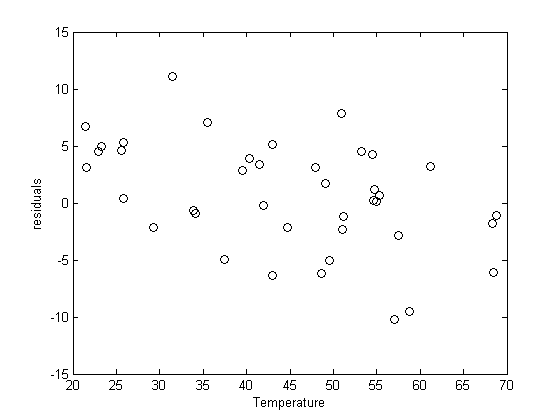
plot residuals
You can see a slight trend of decreasing value of the residuals as the Temperature increases. This may indicate a deficiency in the model with no intercept. For the ideal gas law in degC: 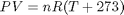 or
or 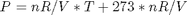 , so the intercept is expected to be non-zero in this case. That is an example of the deficiency.
, so the intercept is expected to be non-zero in this case. That is an example of the deficiency.
residuals = P - X*b; figure plot(T,residuals,'ko') xlabel('Temperature') ylabel('residuals')
'done' % categories: data analysis
ans = done
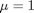 , and
, and  .
.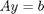 , where
, where  and
and  are defined as follows.
are defined as follows.

 , and we have the following data:
, and we have the following data: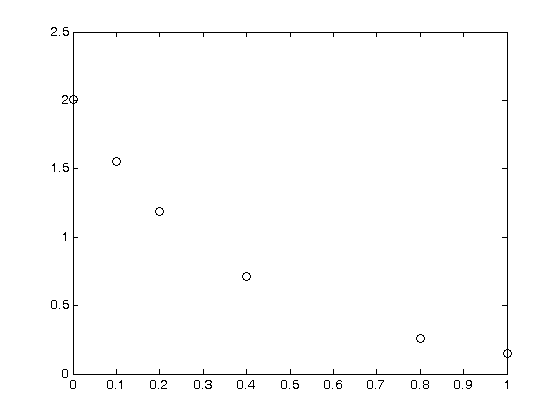
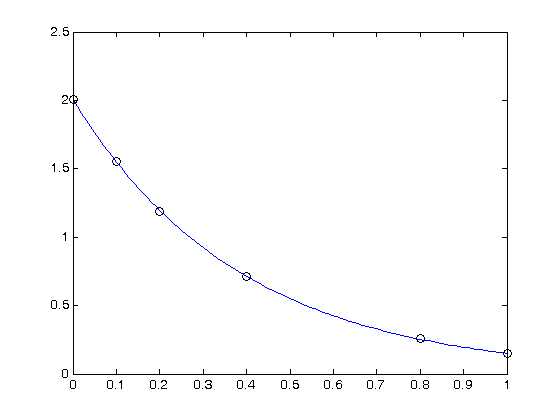
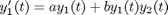
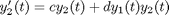
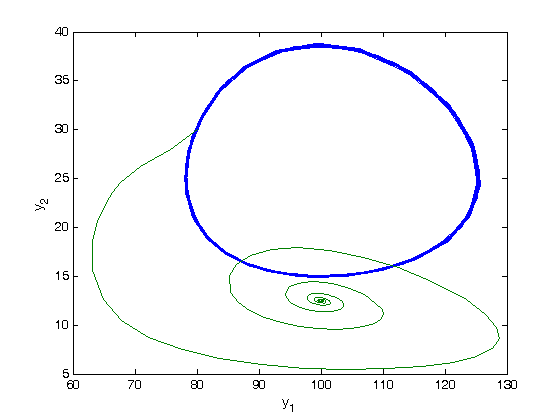
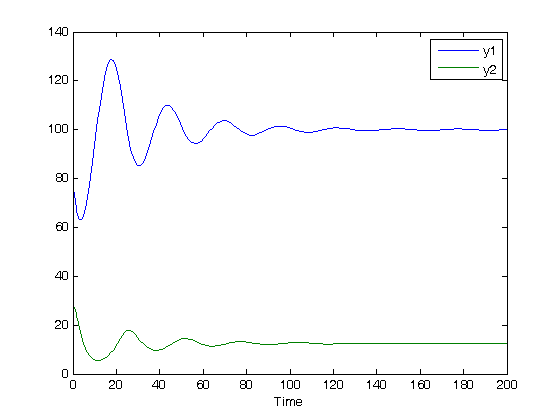
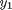 and
and 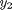 are the prey and predators. These are ordinary differential equations that are straightforward to solve.
are the prey and predators. These are ordinary differential equations that are straightforward to solve. , we can arrive at a new set of delay differential equations:
, we can arrive at a new set of delay differential equations: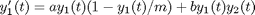
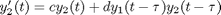
 depends on the value of the solution some time
depends on the value of the solution some time 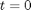 , we have to know the history to know the initial derivative is. We use the dde23 function in Matlab to solve this problem.
, we have to know the history to know the initial derivative is. We use the dde23 function in Matlab to solve this problem.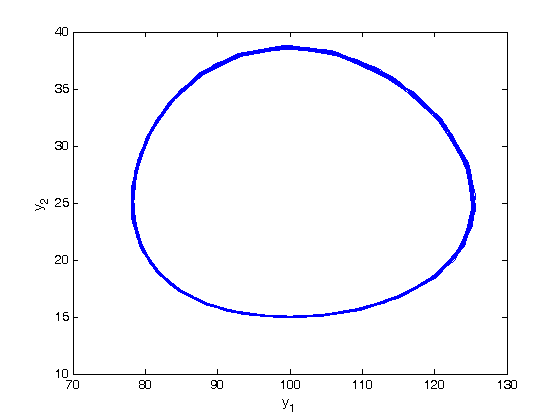
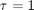 .
.