Controlling the exit concentration of a CSTR
November 13, 2011 at 04:17 PM | categories: miscellaneous | View Comments
Controlling the exit concentration of a CSTR
John Kitchin
We examine how to model a CSTR with a controller that varies the volumetric flowrate to control the exit concentration. First we examine a case with no control, then with a simple controller, and then the response of the controller to a change in temperature which modifies the reaction rate.
function main
close all, clc, clear all V = 100; % volume of CSTR vo = 20; % volumetric flow rate Cain = 2; Ca0 = 2; tspan = linspace(0,20,20*60); % this is the solution at every second. function dCadt = cstr(t,Ca) % A -> B ra = -0.1*Ca; dCadt = Cain - Ca + ra*V/vo ; end [t,Ca] = ode45(@cstr,tspan,Ca0); subplot(2,1,1) plot(t,Ca) xlabel('Time') ylabel('C_A') subplot(2,1,2) plot(tspan,vo,'b.') xlabel('time') ylabel('volumetric flow')
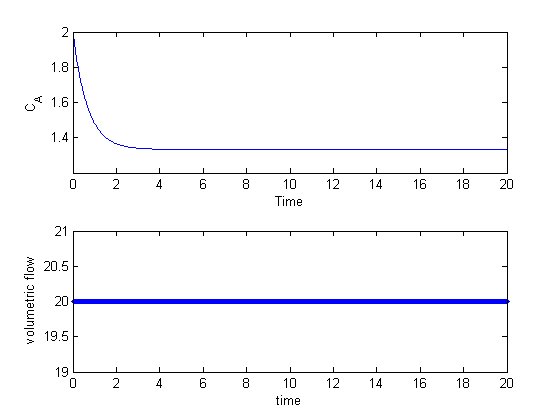
The reactor does not have the desired behavior; the exit concentration is too high. We could simply compute the flow rate required to get the desired exit concentration, but that will only work for this specific set of conditions. If the reactor gets hotter or colder, it will no longer have the desired exit concentration because the reaction rates will change.
Let's implement a controller to actively control the exit concentration by varying the volumetric flow. We will use a simple idea: if the exit concentration is not equal to the desired setpoint, we adjust the volumetric flow by an amount proportional to the difference. We call the proportionality the gain. The choice of the gain factor can have a major impact on the controller. If it is too low, it takes a long time for the system to respond, and if it is too high, the controller may actually be unstable. Here we use a gain that works ok, which we discovered by trial and error. There are ways to determine an optimal behavior that are beyond the scope of this post.
We choose an exit goal of 0.5 mol A/L, corresponding to a conversion of 0.75 for the inlet concentration.
function vo_in = controller(t,Ca) % a simple proportional controller that adjusts the volumetric % flow by an amount proportional to the deviation between the % desired and actual exit concentrations. setpoint = 0.5; % desired exit concentration error = setpoint - Ca; gain = 0.5; vo = vo + gain*error; % We don't want to allow vo to be negative, and practically it % cannot be zero either, since then tau = infinity. Our pump is % also limited to a maximum volumetric flow of 40. if vo < 0.001; vo = 0.001 elseif vo > 40 vo = 40; end % let's plot the volumetric flow to see how it changes everytime % this function is called. subplot(2,1,2); hold on plot(t,vo,'b.') vo_in = vo; end function dCadt = controlled_cstr(t,Ca) % A -> B ra = -0.1*Ca; % the next line sets the volumetric flow. vo = controller(t,Ca); dCadt = Cain - Ca + ra*V/vo ; end tspan = linspace(20,40,20*60); init = Ca(end); % start at the end of the last integration [t2,Ca2] = ode45(@controlled_cstr,tspan,init); subplot(2,1,1); hold on plot(t2,Ca2,'r-')
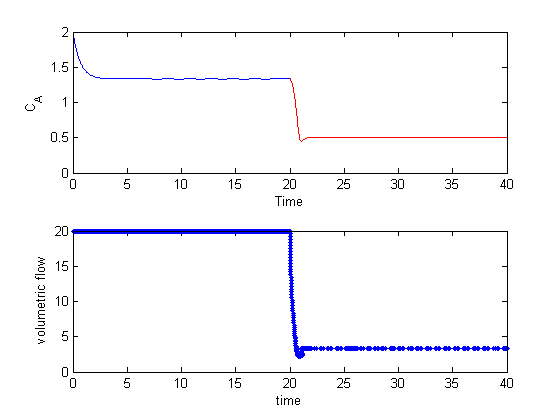
The controller quickly decreases the volumetric flowrate to increase the residence time, resulting in a decrease in exit concentration. Here you can see the gain is a little too high, because the controller overshoots and the exit concentration, and there are some excursions from the setpoint after that. Those are due to numerical errors in the ODE integration.
Now let's see how the controller responds to a temperature excursion. Suppose the reactor cools down, and the reaction rate is suddenly one half the rate it used to be. The exit concentration will rise, since the reactants are not reacting as fast. The controller should decrease the volumetric flowrate to increase the space time.
function dCadt = controlled_cstr_temperature(t,Ca) % A -> B ra = -0.05*Ca; vo = controller(t,Ca); dCadt = Cain - Ca + ra*V/vo ; end tspan = linspace(40,60,20*60); init = Ca2(end); % start at the end of the last integration [t3,Ca3] = ode45(@controlled_cstr_temperature,tspan,init); subplot(2,1,1); hold on plot(t3,Ca3,'k-')
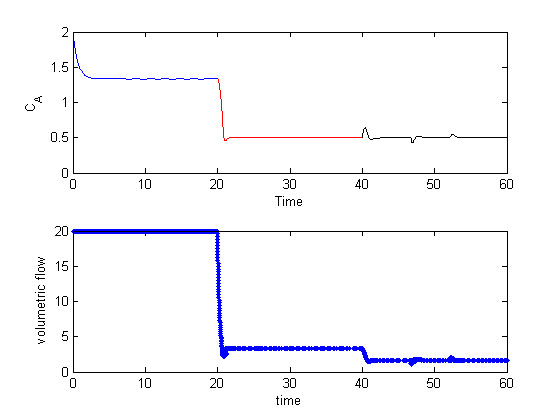
As expected, the concentration initially goes up, then the controller lowers the volumetric flowrate. Also note the controller was able to keep the exit concentration at the setpoint even though the rate of the reaction changed due to the temperature change. There are some notable small deviations from the setpoint near times 47 and 52. These are due to the ODE solver. If you examine the spacing of the points in the volumetric flow graph you will see they are not evenly spaced at 1 sec. That is because the volumetric flow is updated for every call to the ode function, not just at the solution points.
Now that I have tried this, it is clear this is not the best way to model the effect of a controller, because the ODE integrator does some funny things with the time steps. Sometimes the solver appears to take steps back in time to improve the accuracy of the solution, but that is not physically real, and the controller doesn't account for this non-physical behavior. That is why, for example there are excursions from the setpoint after an apparent steady state value is reached in the last example. Maybe this is why everyone uses Simulink for control problems!
end % categories: Miscellaneous % tags: control % post_id = 1460; %delete this line to force new post; % permaLink = http://matlab.cheme.cmu.edu/2011/11/13/control_cstr-m/;

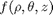 that is the solution to the following set of equations:
that is the solution to the following set of equations: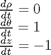
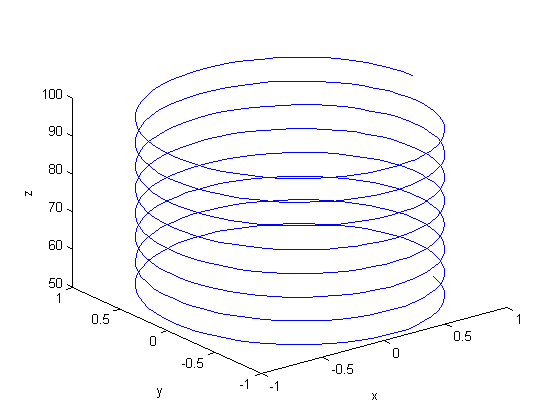
![$f(0,0,0) = [0,0, 100]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/11/plot_cylindrical_ode_soln_eq521161.png) . There is nothing special about these equations; they describe a cork screw with constant radius. Solving the equations is simple; they are not coupled, and we simply integrate each equation with ode45. Plotting the solution is trickier, because we have to convert the solution from cylindrical coordinates to cartesian coordinates for plotting.
. There is nothing special about these equations; they describe a cork screw with constant radius. Solving the equations is simple; they are not coupled, and we simply integrate each equation with ode45. Plotting the solution is trickier, because we have to convert the solution from cylindrical coordinates to cartesian coordinates for plotting.