plot the solution to an ODE in cylindrical coordinates

John Kitchin

Matlab provides pretty comprehensive support to plot functions in cartesian coordinates. There is no direct support to plot in cylindrical coordinates, however. In this post, we learn how to solve an ODE in cylindrical coordinates, and to plot the solution in cylindrical coordinates.

We want the function 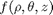that is the solution to the following set of equations:

Contents

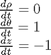
with initial conditions . There is nothing special about these equations; they describe a cork screw with constant radius. Solving the equations is simple; they are not coupled, and we simply integrate each equation with ode45. Plotting the solution is trickier, because we have to convert the solution from cylindrical coordinates to cartesian coordinates for plotting.

function main

    function dfdt = cylindrical_ode(t,F)
        rho = F(1);
        theta = F(2);
        z = F(3);

        drhodt = 0; % constant radius
        dthetadt = 1; % constant angular velocity
        dzdt = -1; % constant dropping velocity
        dfdt = [drhodt; dthetadt; dzdt];
    end

rho0 = 1;
theta0 = 0;
z0 = 100;

tspan = linspace(0,50,500);
[t,f] = ode45(@cylindrical_ode,tspan,[rho0 theta0 z0]);

rho = f(:,1);
theta = f(:,2);
z = f(:,3);

plot3(rho,theta,z)
xlabel('x')
ylabel('y')
zlabel('z')

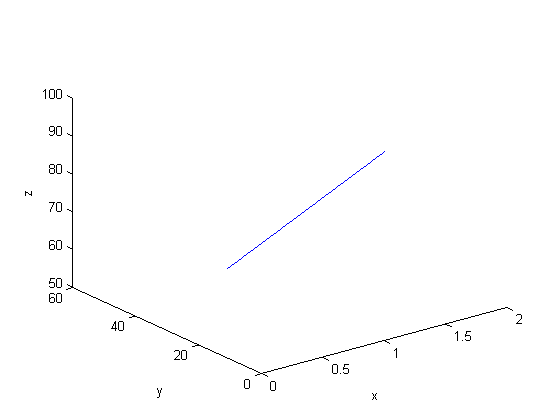
This is not a cork screw at all! The problem is that plot3 expects cartesian coordinates, but we plotted cylindrical coordinates. To use the plot3 function we must convert the cylindrical coordinates to cartesian coordinates. Matlab provides a simple utility for doing that.

Convert the cylindrical coordinates to cartesian coordinates

[X Y Z] = pol2cart(theta,rho,z);

plot3(X,Y,Z)
xlabel('x')
ylabel('y')
zlabel('z')

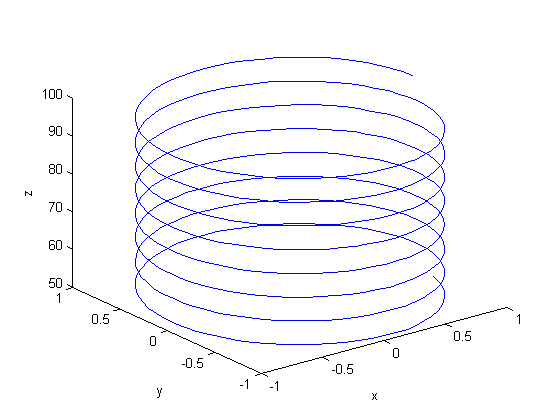
That is the corkscrew we were expecting! The axes are still the x,y,z axes. It doesn't make sense to label them anything else.

end

% categories: ODEs, plotting
% tags: math

Published with MATLAB® 7.12