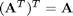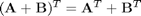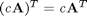Contents

Plot customizations - Modifying line, text and figure properties

John Kitchin

The plot command allows you to specify many properties of the lines in your plots, e.g. the line color, width, and style, and the marker properties. For presentations, it is usually a good idea to use thicker lines so they are easy to see from a projector. Here we examine some ways to do that.

close all; clear all; clc

x1 = 0:0.1:2*pi;
y1 = sin(x1);

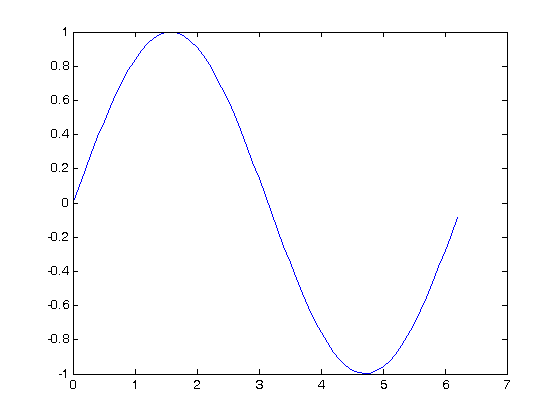
The vanilla plot

plot(x1,y1)

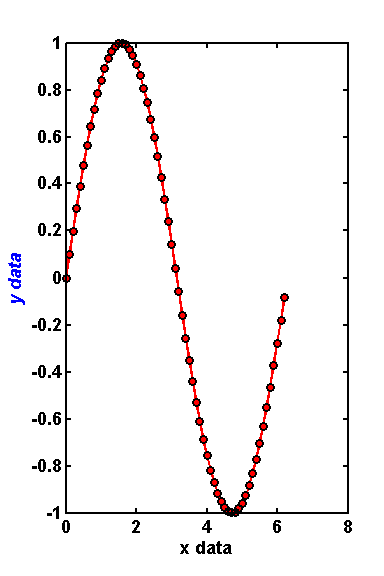
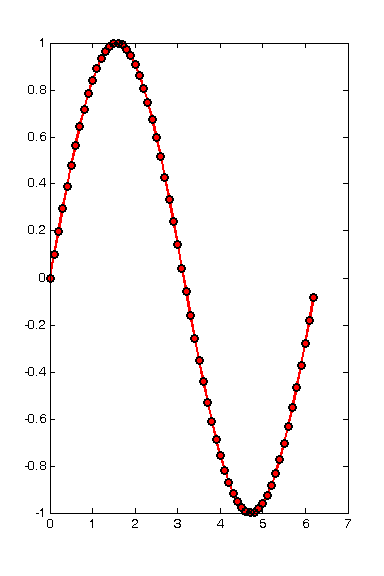
Customized plot

Lets increase the line thickness, change the line color to red, and make the markers red circles with black outlines. I also like figures in presentations to be 6 inches high, and 4 inches wide.

width = 4;
height = 6;
figure('Units','inches','Position',[1 1 width height])
plot(x1,y1,...
    'linewidth',2,...
    'color','r',...
    'marker','o',...
    'markeredgecolor','k',...
    'markerfacecolor','r')

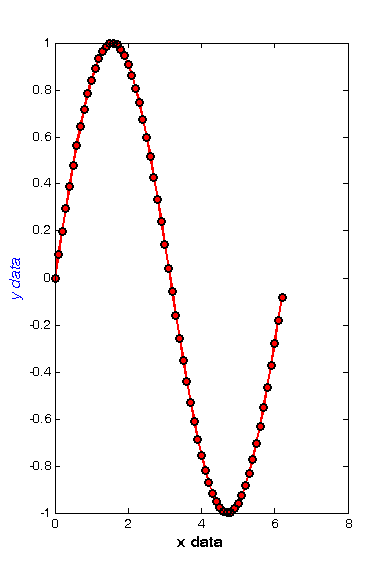
customizing the axis labels

sometimes it is nice to change the size and style of the label text.

xlabel('x data','fontsize',12,'fontweight','bold')
ylabel('y data','fontsize',12,'fontangle','italic','color','b')

See this page for a listing of all the text properties you can set. http://www.mathworks.com/help/techdoc/ref/text_props.html

setting all the text properties in a figure.

you may notice the axis tick labels are not consistent with the labels now. If you have many plots it can be tedious to try setting each text property. Matlab to the rescue! With these commands you can find all the text instances, and change them all at one time! Likewise, you can change all the lines, and all the axes.

a=findobj(gcf); % get the handles associated with the current figure

allaxes=findall(a,'Type','axes');
alllines=findall(a,'Type','line');
alltext=findall(a,'Type','text');

set(allaxes,'FontName','Arial','FontWeight','Bold','LineWidth',2,...
    'FontSize',14);
set(alllines,'Linewidth',2);
set(alltext,'FontName','Arial','FontWeight','Bold','FontSize',14);

% categories: Plotting

% post_id = 588; %delete this line to force new post;

Published with MATLAB® 7.10

Illustrating matrix transpose rules in matrix multiplication

John Kitchin

Contents

Rules for transposition

Here are the four rules for matrix multiplication and transposition

1.

2.

3.

4.

reference: Chapter 7.2 in Advanced Engineering Mathematics, 9th edition. by E. Kreyszig.

The transpose in Matlab

there are two ways to get the transpose of a matrix: with a notation, and with a function

A = [[5 -8 1];
    [4 0 0]]

A =

     5    -8     1
     4     0     0

function

transpose(A)

ans =

     5     4
    -8     0
     1     0

notation

A.'

% note, these functions only provide the non-conjugate transpose. If your
% matrices are complex, then you want the ctranspose function, or the
% notation A' (no dot before the apostrophe). For real matrices there is no
% difference between them.

% below we illustrate each rule using the different ways to get the
% transpose.

ans =

     5     4
    -8     0
     1     0

Rule 1

m1 = (A.').'
A

all(all(m1 == A)) % if this equals 1, then the two matrices are equal

m1 =

     5    -8     1
     4     0     0


A =

     5    -8     1
     4     0     0


ans =

     1

Rule 2

B = [[3 4 5];
    [1 2 3]];
m1 = transpose(A+B)
m2 = transpose(A) + transpose(B)

all(all(m1 == m2)) % if this equals 1, then the two matrices are equal

m1 =

     8     5
    -4     2
     6     3


m2 =

     8     5
    -4     2
     6     3


ans =

     1

Rule 3

c = 2.1;
m1 = transpose(c*A)
m2 = c*transpose(A)

all(all(m1 == m2)) % if this equals 1, then the two matrices are equal

m1 =

   10.5000    8.4000
  -16.8000         0
    2.1000         0


m2 =

   10.5000    8.4000
  -16.8000         0
    2.1000         0


ans =

     1

Rule 4

B = [[0 2];
    [1 2];
    [6 7]]

m1 = (A*B).'
m2 = B.'*A.'

all(all(m1 == m2)) % if this equals 1, then the two matrices are equal

B =

     0     2
     1     2
     6     7


m1 =

    -2     0
     1     8


m2 =

    -2     0
     1     8


ans =

     1

m3 = A.'*B.'
% you can see m3 has a different shape than m1, so there is no way they can
% be equal.

m3 =

     8    13    58
     0    -8   -48
     0     1     6

% categories: Linear algebra
% tags: math
% post_id = 552; %delete this line to force new post;

Published with MATLAB® 7.10