Illustrating matrix transpose rules in matrix multiplication

John Kitchin

Contents

Rules for transposition

Here are the four rules for matrix multiplication and transposition

1.

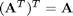
2.

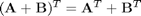
3.

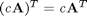
4.

reference: Chapter 7.2 in Advanced Engineering Mathematics, 9th edition. by E. Kreyszig.

The transpose in Matlab

there are two ways to get the transpose of a matrix: with a notation, and with a function

A = [[5 -8 1];
    [4 0 0]]

A =

     5    -8     1
     4     0     0

function

transpose(A)

ans =

     5     4
    -8     0
     1     0

notation

A.'

% note, these functions only provide the non-conjugate transpose. If your
% matrices are complex, then you want the ctranspose function, or the
% notation A' (no dot before the apostrophe). For real matrices there is no
% difference between them.

% below we illustrate each rule using the different ways to get the
% transpose.

ans =

     5     4
    -8     0
     1     0

Rule 1

m1 = (A.').'
A

all(all(m1 == A)) % if this equals 1, then the two matrices are equal

m1 =

     5    -8     1
     4     0     0


A =

     5    -8     1
     4     0     0


ans =

     1

Rule 2

B = [[3 4 5];
    [1 2 3]];
m1 = transpose(A+B)
m2 = transpose(A) + transpose(B)

all(all(m1 == m2)) % if this equals 1, then the two matrices are equal

m1 =

     8     5
    -4     2
     6     3


m2 =

     8     5
    -4     2
     6     3


ans =

     1

Rule 3

c = 2.1;
m1 = transpose(c*A)
m2 = c*transpose(A)

all(all(m1 == m2)) % if this equals 1, then the two matrices are equal

m1 =

   10.5000    8.4000
  -16.8000         0
    2.1000         0


m2 =

   10.5000    8.4000
  -16.8000         0
    2.1000         0


ans =

     1

Rule 4

B = [[0 2];
    [1 2];
    [6 7]]

m1 = (A*B).'
m2 = B.'*A.'

all(all(m1 == m2)) % if this equals 1, then the two matrices are equal

B =

     0     2
     1     2
     6     7


m1 =

    -2     0
     1     8


m2 =

    -2     0
     1     8


ans =

     1

m3 = A.'*B.'
% you can see m3 has a different shape than m1, so there is no way they can
% be equal.

m3 =

     8    13    58
     0    -8   -48
     0     1     6

% categories: Linear algebra
% tags: math
% post_id = 552; %delete this line to force new post;

Published with MATLAB® 7.10