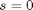Modeling a transient plug flow reactor
November 17, 2011 at 02:35 PM | categories: pdes | View Comments
Modeling a transient plug flow reactor
John Kitchin
Contents


function main
clear all; clc; close all function dCdt = method_of_lines(t,C) % we use vectorized operations to define the odes at each node % point. dCdt = [0; % C1 does not change with time, it is the entrance of the pfr -vo*diff(C)./diff(V)-k*C(2:end).^2]; end
Problem setup
Ca0 = 2; % Entering concentration vo = 2; % volumetric flow rate volume = 20; % total volume of reactor, spacetime = 10 k = 1; % reaction rate constant N = 100; % number of points to discretize the reactor volume on init = zeros(N,1); % Concentration in reactor at t = 0 init(1) = Ca0; % concentration at entrance V = linspace(0,volume,N)'; % discretized volume elements, in column form tspan = [0 20]; [t,C] = ode15s(@method_of_lines,tspan,init);
plotting the solution
The solution contains the time dependent behavior of each node in the discretized reactor. For example, we can plot the concentration of A at the exit vs. time as:
plot(t,C(:,end)) xlabel('time') ylabel('Concentration at exit')
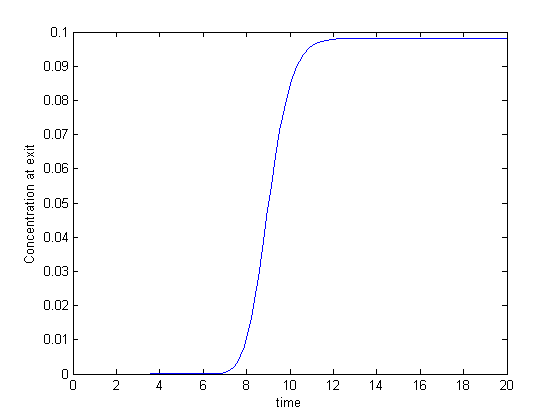
You can see that around the space time, species A breaks through the end of the reactor, and rapidly rises to a steady state value.
animating the solution
It isn't really illustrative to examine only the exit concentration. We can also create an animated gif to show how the concentration of A throughout the reactor varies with time.
filename = 'transient-pfr.gif'; % file to store image in for i=1:5:length(t) % only look at every 5th time step plot(V,C(i,:)); ylim([0 2]) xlabel('Reactor volume') ylabel('C_A') text(0.1,1.9,sprintf('t = %1.2f',t(i))); % add text annotation of time step frame = getframe(1); im = frame2im(frame); %convert frame to an image [imind,cm] = rgb2ind(im,256); % now we write out the image to the animated gif. if i == 1; imwrite(imind,cm,filename,'gif', 'Loopcount',inf); else imwrite(imind,cm,filename,'gif','WriteMode','append'); end end close all; % makes sure the plot from the loop above doesn't get published
here is the animation!
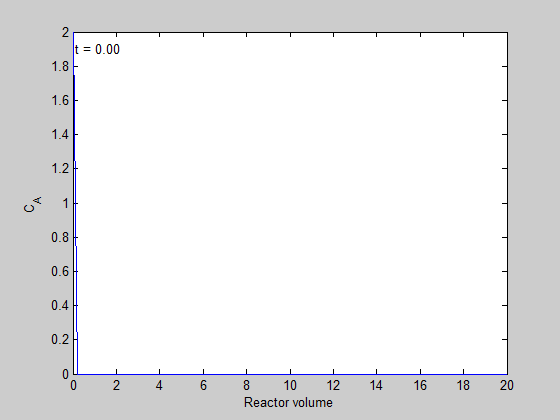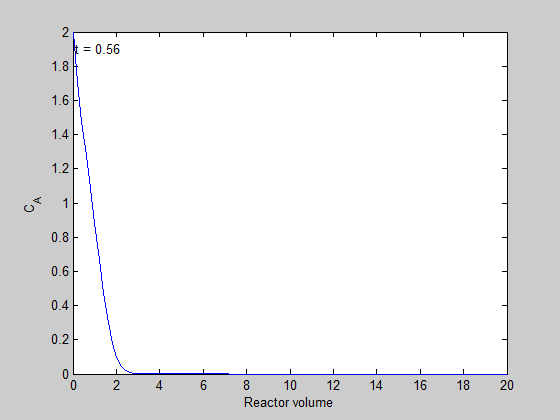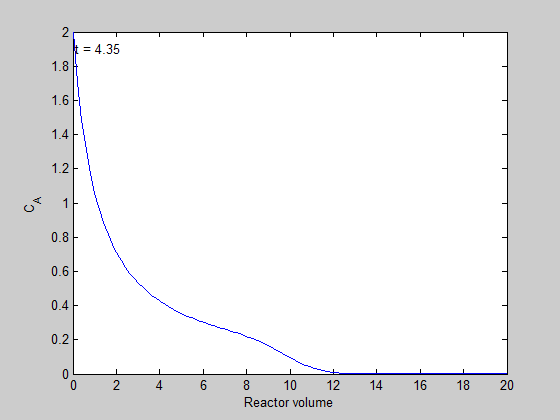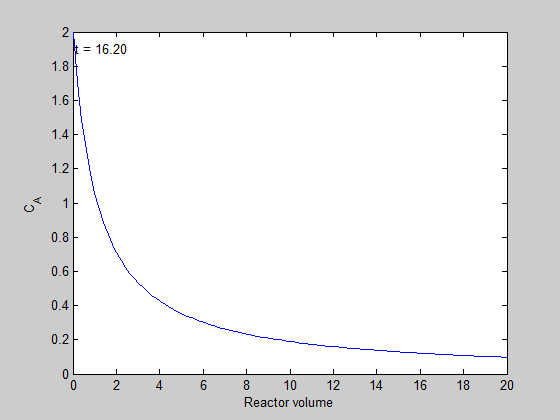
You can see that the steady state behavior is reached at approximately 10 time units, which is the space time of the reactor in this example.
Add steady state solution
It is good to double check that we get the right steady state behavior. We can solve the steady state plug flow reactor problem like this:
function dCdV = pfr(V,C) dCdV = 1/vo*(-k*C^2); end figure; hold all vspan = [0 20]; [V_ss Ca_ss] = ode45(@pfr,vspan,2); plot(V_ss,Ca_ss,'k--','linewidth',2) plot(V,C(end,:),'r') % last solution of transient part legend 'Steady state solution' 'transient solution at t=100'
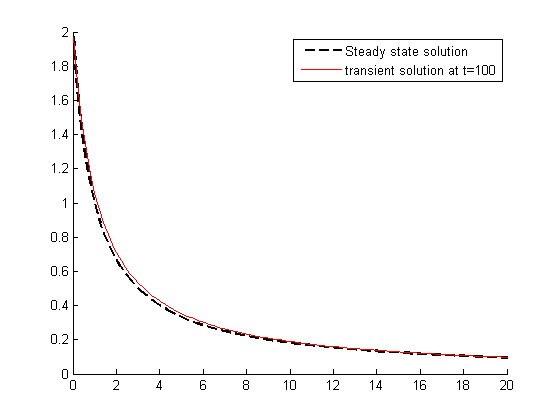
there is some minor disagreement between the final transient solution and the steady state solution. That is due to the approximation in discretizing the reactor volume. In this example we used 100 nodes. You get better agreement with a larger number of nodes, say 200 or more. Of course, it takes slightly longer to compute then, since the number of coupled odes is equal to the number of nodes.
end % categories: PDEs % tags: reaction engineering
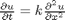
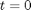 , in this example we have
, in this example we have 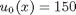 as an initial condition. with boundary conditions
as an initial condition. with boundary conditions 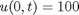 and
and 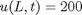 .
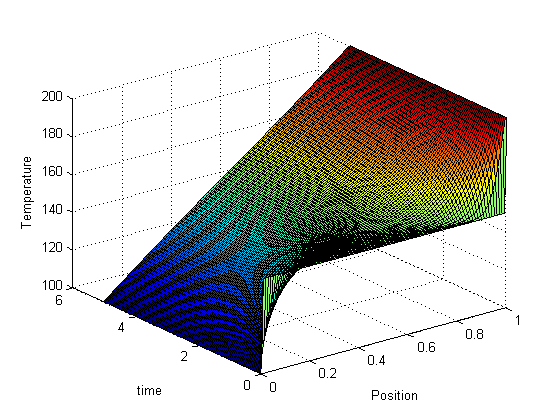
.
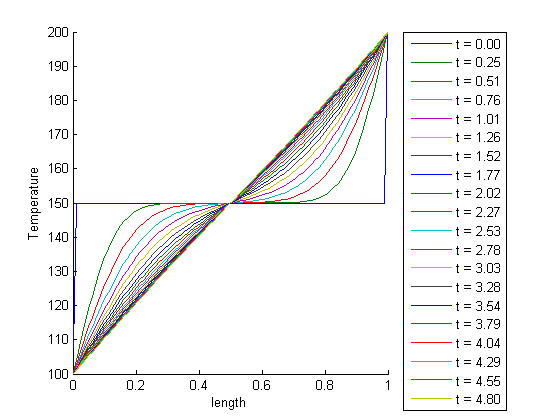
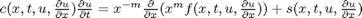
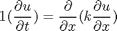
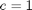 ,
,  , and
, and