Linear programming example with inequality constraints
October 21, 2011 at 10:33 PM | categories: optimization | View Comments
Linear programming example with inequality constraints
John Kitchin
adapted from http://www.matrixlab-examples.com/linear-programming.html which solves this problem with fminsearch.
Let's suppose that a merry farmer has 75 roods (4 roods = 1 acre) on which to plant two crops: wheat and corn. To produce these crops, it costs the farmer (for seed, water, fertilizer, etc. ) $120 per rood for the wheat, and $210 per rood for the corn. The farmer has $15,000 available for expenses, but after the harvest the farmer must store the crops while awaiting favorable or good market conditions. The farmer has storage space for 4,000 bushels. Each rood yields an average of 110 bushels of wheat or 30 bushels of corn. If the net profit per bushel of wheat (after all the expenses) is $1.30 and for corn is $2.00, how should the merry farmer plant the 75 roods to maximize profit?
Let x be the number of roods of wheat planted, and y be the number of roods of corn planted. The profit function is: P = (110)($1.3)x + (30)($2)y = 143x + 60y
There are some constraint inequalities, specified by the limits on expenses, storage and roodage. They are:
$120x + $210y <= $15000 % The total amount spent can't exceed the amount the farm has.
110x + 30y <= 4000 % The amount generated should not exceed storage space.
x + y <= 75 % We can't plant more space than we have.
0 <= x and 0 <= y % all amounts of planted land must be positive.
Contents
Function to minimize
To solve this problem, we cast it as a linear programming problem, which minimizes a function f(X) subject to some constraints. We create a proxy function for the negative of profit, which we seek to minimize.
f = -143*x - 60*y
f = [-143 -60];
Inequality constraints
We express our constraints in the form A*x <= b
120x + 210y <= 15000 110x + 30y <= 4000 x + y <= 75
A = [120 210
110 30
1 1];
b = [15000
4000
75];
Lower bounds
Finally, we express the lower bounds on the unknowns. 0 <= x and 0 <= y
lb = [0
0];
Finally solve the problem
[X,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb); fprintf('We should plant %1.2f roods of wheat.\n',X(1)) fprintf('We should plant %1.2f roods of corn.\n',X(2)) profit = -f*X; fprintf('The maximum profit we can earn is $%1.2f.',profit) % categories: optimization
Optimization terminated. We should plant 21.88 roods of wheat. We should plant 53.12 roods of corn. The maximum profit we can earn is $6315.62.
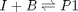
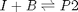
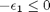
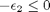
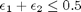
![$A = \left[ \begin{array}{cc} -1 & 0 \\ 0 & -1 \\ 1 & 1 \end{array} \right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/08/Gmin_eq10921.png) and
and ![$b = \left[ \begin{array}{c} 0 \\ 0 \\ 0.5\end{array} \right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/08/Gmin_eq62028.png)