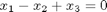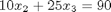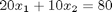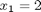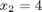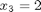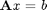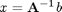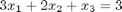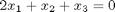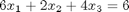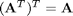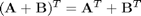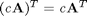Sums, products and linear algebra notation - avoiding loops where possible
January 03, 2012 at 05:03 PM | categories: linear algebra | View Comments
Sums, products and linear algebra notation - avoiding loops where possible
John Kitchin
Today we examine some methods of linear algebra that allow us to avoid writing explicit loops in Matlab for some kinds of mathematical operations.
Contents
Consider the operation on two vectors  and
and 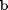 .
.
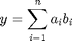
a = [1 2 3 4 5]; b = [3 6 8 9 10];
Old-fashioned way with a loop
We can compute this with a loop, where you initialize y, and then add the product of the ith elements of a and b to y in each iteration of the loop. This is known to be slow for large vectors
y = 0; for i=1:length(a) y = y + a(i)*b(i); end y
y = 125
dot notation
Matlab defines dot operators, so we can compute the element-wise product of  and
and 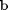 , and then use the builtin sum command to get the result.
, and then use the builtin sum command to get the result.
y = sum(a.*b)
y = 125
dot product
The operation above is formally the definition of a dot product. We can directly compute this in Matlab. Note that one vector must be transposed so that we have the right dimensions for legal matrix multiplication (one vector must be a row, and one must be column). It does not matter which order the multiplication is done as shown here.
y = a*b' y = b*a'
y = 125 y = 125
Another example
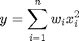
This operation is like a weighted sum of squares.
w = [0.1 0.25 0.12 0.45 0.98]; x = [9 7 11 12 8];
Old-fashioned method with a loop
y = 0; for i = 1:length(w) y = y + w(i)*x(i)^2; end y
y = 162.3900
dot operator approach
We use parentheses to ensure that x is squared element-wise before the element-wise multiplication.
y = sum(w.*(x.^2))
y = 162.3900
Linear algebra approach
The operation is mathematically equivalent to 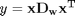 when
when  is a row vector.
is a row vector. 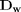 is a diagonal matrix with the values of
is a diagonal matrix with the values of  on the diagonal, and zeros everywhere else. The Matlab command diag creates this matrix conveniently.
on the diagonal, and zeros everywhere else. The Matlab command diag creates this matrix conveniently.
y = x*diag(w)*x'
y = 162.3900
Last example
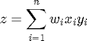
This operation is like a weighted sum of products.
w = [0.1 0.25 0.12 0.45 0.98]; x = [9 7 11 12 8]; y = [2 5 3 8 0];
Old fashioned method with a loop
z = 0; for i=1:length(w) z = z + w(i)*x(i)*y(i); end z
z = 57.7100
dot notation
we use parentheses
z = sum(w.*x.*y)
z = 57.7100
Linear algebra approach
Note that it does not matter what order the dot products are done in, just as it does not matter what order w(i)*x(i)*y(i) is multiplied in.
z = x*diag(w)*y' z = y*diag(x)*w' z = w*diag(y)*x'
z = 57.7100 z = 57.7100 z = 57.7100
Summary
We showed examples of the following equalities between traditional sum notations and linear algebra
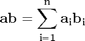
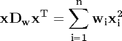
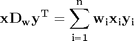
These relationships enable one to write the sums as a single line of Matlab code, which utilizes fast linear algebra subroutines, avoids the construction of slow loops, and reduces the opportunity for errors in the code. Admittedly, it introduces the opportunity for new types of errors, like using the wrong relationship, or linear algebra errors due to matrix size mismatches.
% categories: Linear Algebra % tags: math
 matrix
matrix
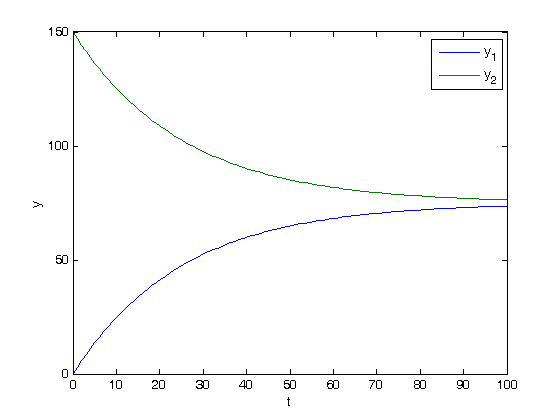
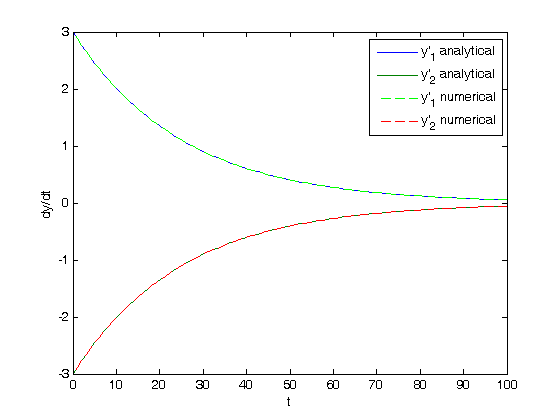
![$\left[\begin{array}{c}y'_1\\y'_2\end{array}\right] = \left[\begin{array}{cc} -0.02 & 0.02 \\ 0.02 & -0.02\end{array}\right] \left[\begin{array}{c}y_1\\y_2\end{array}\right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/10/const_coeff_coupled_eq84697.png)
![$\left[\begin{array}{c}y_1\\y_2\end{array}\right] = \left[\begin{array}{cc}v_1 & v_2\end{array}\right] \left[\begin{array}{cc} c_1 & 0 \\ 0 & c_2\end{array}\right] \exp\left(\left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2\end{array}\right] \left[\begin{array}{c}t\\t\end{array}\right]\right)$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/10/const_coeff_coupled_eq32208.png)
![$\left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2\end{array}\right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/10/const_coeff_coupled_eq06652.png) is a diagonal matrix of the eigenvalues of the constant coefficient matrix,
is a diagonal matrix of the eigenvalues of the constant coefficient matrix, ![$\left[\begin{array}{cc}v_1 & v_2\end{array}\right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/10/const_coeff_coupled_eq51102.png) is a matrix of eigenvectors where the
is a matrix of eigenvectors where the  column corresponds to the eigenvector of the
column corresponds to the eigenvector of the ![$\left[\begin{array}{cc} c_1 & 0 \\ 0 & c_2\end{array}\right]$](http://matlab.cheme.cmu.edu/wp-content/uploads/2011/10/const_coeff_coupled_eq84783.png) is a matrix determined by the initial conditions.
is a matrix determined by the initial conditions.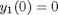 and
and 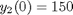 .
. matrix
matrix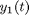 and
and 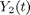 .
.