Reading parameter database text files in Matlab

September 10, 2011 at 06:31 PM | categories: file io | View Comments

read_use_antoine

Contents

Reading parameter database text files in Matlab

John Kitchin

clear all; clc; close all

the datafile at http://terpconnect.umd.edu/~nsw/ench250/antoine.dat contains data that can be used to estimate the vapor pressure of about 700 pure compounds using the Antoine equation

The data file has the following contents:

 Antoine Coefficients
   log(P) = A-B/(T+C) where P is in mmHg and T is in Celsius
 Source of data: Yaws and Yang (Yaws, C.  L.  and Yang, H.  C.,
 "To estimate vapor pressure easily. antoine coefficients relate vapor pressure to temperature for almost 700 major organic compounds", Hydrocarbon Processing, 68(10), p65-68, 1989.
 ID  formula  compound name                  A       B       C     Tmin Tmax ??    ?
 -----------------------------------------------------------------------------------
   1 CCL4     carbon-tetrachloride        6.89410 1219.580 227.170  -20  101 Y2    0
   2 CCL3F    trichlorofluoromethane      6.88430 1043.010 236.860  -33   27 Y2    0

To use this data, you find the line that has the compound you want, and read off the data. You could do that manually for each component you want but that is tedious, and error prone. Today we will see how to retrieve the file, then read the data into Matlab to create a database we can use to store and retrieve the data.

We will use the data to find the temperature at which the vapor pressure of acetone is 400 mmHg.

get a local copy of the file

urlwrite('http://terpconnect.umd.edu/~nsw/ench250/antoine.dat','antoine_data.dat');

Reading in the data

We use the textscan command to skip the first 7 header lines, and then to parse each line according to the format string. After the header, each line has the format of:

 integer string string float float float float float string string

which we represent by '%d%s%s%f%f%f%f%f%s%s' as a format string. Note we are basically ignoring the contents of the last two columns, and just reading them in as strings. The output of the textread command will be a vector of values for each numerical column, and a cell array for string data.

now open it, and read it

the output of the textscan command is a cell array of all the data read in.

fid = fopen('antoine_data.dat');
C = textscan(fid,'%d%s%s%f%f%f%f%f%s%s','headerlines',7);
fclose(fid);

convert the cell array output of textscan into variables

This makes it easier to read the code where we assign the database. Each of these varialbes is a column vector containing the data for that column in our text file.

[id formula compound A B C Tmin Tmax i j] = C{:};

the database

the Map object will let us refer to an entry as database('acetone')

database = containers.Map();

storing the data

for i=1:length(id)
    % we store the data as a cell for each compound
    database(compound{i}) = {A(i) B(i) C(i) Tmin(i) Tmax(i)};
end
% That's it! Now, we can use the database to retrieve specific entries.

Now use the database to plot the vapor pressure of acetone

get the parameters for acetone

compound = database('acetone')
% for readability let's pull out each data property into variable names
[A B C Tmin Tmax] = compound{:}

compound = 

    [7.2316]    [1.2770e+003]    [237.2300]    [-32]    [77]


A =

    7.2316


B =

  1.2770e+003


C =

  237.2300


Tmin =

   -32


Tmax =

    77

plot vapor pressure of acetone over the allowable temperature range.

T = linspace(Tmin, Tmax);
P = 10.^(A - B./(T+C));
plot(T,P)
xlabel('T (\circC)')
ylabel('P_{vap} (mmHg)')

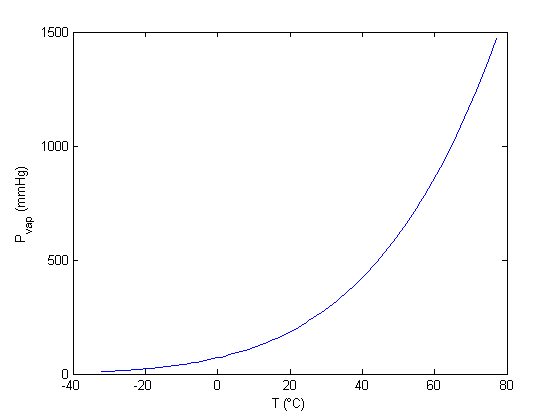
Find T at which Pvap = 400 mmHg

from our graph we might guess T ~ 40 degC

Tguess = 40;
f = @(T) 400 - 10.^(A - B./(T+C));
T400 = fzero(f,Tguess)

sprintf('The vapor pressure is 400 mmHg at T = %1.1f degC',T400)

T400 =

   38.6138


ans =

The vapor pressure is 400 mmHg at T = 38.6 degC

This result is close to the value reported here (39.5 degC), from the CRC Handbook. The difference is probably that the value reported in the CRC is an actual experimental number.

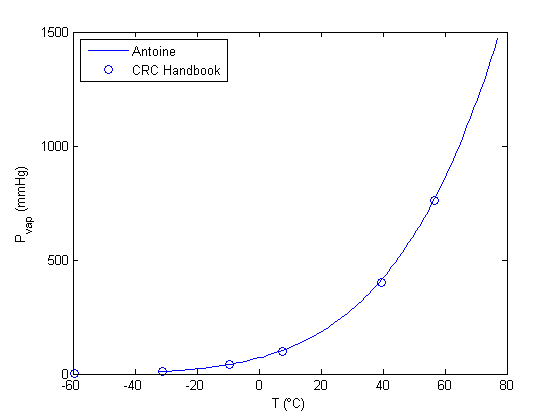
Plot CRC data

We only include the data for the range where the Antoine fit is valid.

T  = [-59.4 	-31.1 	-9.4 	7.7 	39.5 	56.5];
P = [	1 	10 	40 	100 	400 	760];

hold all
plot(T,P,'bo')
legend('Antoine','CRC Handbook','location','northwest')
% There is pretty good agreement between the Antoine equation and the data.

save the database for later use.

we can load this file into Matlab at a later time instead of reading in the text file again.

save  antoine_database.mat database

% categories: File IO
% tags: thermodynamics


Published with MATLAB® 7.12

Read and Post Comments

Manipulating excel with Matlab

August 07, 2011 at 09:25 PM | categories: file io | View Comments

Manipulating excel with Matlab

Manipulating excel with Matlab

John Kitchin

Sometimes there is data in an excel sheet that you want to read in, or you may want to write data to a spreadsheet. If you have a sophisticated analysis done in excel, but you want to do some analysis in Matlab, you might want to write data to the worksheet, and then read out the results.

Contents

Example setup

in our spreadsheet ( download example.xlsx ), cell B1 contains a value, and cell B2 contains $B1^2 - 1$. We can read each cell. We can also write a value to B1, and then read B2 to get the value squared. finally, we will create a function that uses Excel to perform the calculation of squaring a number, and use fsolve to minimize the function.

It is a simple example to illustrate a usage. A more realistic example might be an excel sheet where you have a complex design sheet that computes the cost of a unit operation based on properties such as volume, flow rate, etc... and you want to use Matlab to minimize the cost, but Excel to compute the cost. This is not speedy, and you may find it necessary to eventually code the whole analysis in Matlab.

function main

examples of reading

xlsread('example.xlsx','sheet1','b1')
xlsread('example.xlsx','sheet1','b2')

xlswrite('example.xlsx',4,'sheet1','b1')

ans =

     3


ans =

     8


xlsread('example.xlsx','sheet1','b1')
xlsread('example.xlsx','sheet1','b2')
% you can see we did set the value of b1 as we said, and the value of b2 is
% updated also.

ans =

     4


ans =

    15

Find roots

there are two solutions, $\pm 1$. We try guesses above and below each one.

positive root

fsolve(@f,2)
fsolve(@f,0.8)

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

    1.0000


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

    1.0000

negative root

fsolve(@f,-2)
fsolve(@f,-0.8)
% note it is not fast to solve this!

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

   -1.0000


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

   -1.0000

make a plot

x = linspace(-2,2,10);
y = arrayfun(@f,x); %this maps the function f onto the vector x

plot(x,y)
% note that this is also pretty slow.

function y = f(x)
xlswrite('example.xlsx',x,'sheet1','b1');
y = xlsread('example.xlsx','sheet1','b2');

% categories: File IO

% post_id = 739; %delete this line to force new post;


Published with MATLAB® 7.10

Read and Post Comments