Manipulating excel with Matlab

John Kitchin

Sometimes there is data in an excel sheet that you want to read in, or you may want to write data to a spreadsheet. If you have a sophisticated analysis done in excel, but you want to do some analysis in Matlab, you might want to write data to the worksheet, and then read out the results.

Contents

Example setup

in our spreadsheet ( download example.xlsx ), cell B1 contains a value, and cell B2 contains 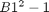. We can read each cell. We can also write a value to B1, and then read B2 to get the value squared. finally, we will create a function that uses Excel to perform the calculation of squaring a number, and use fsolve to minimize the function.

It is a simple example to illustrate a usage. A more realistic example might be an excel sheet where you have a complex design sheet that computes the cost of a unit operation based on properties such as volume, flow rate, etc... and you want to use Matlab to minimize the cost, but Excel to compute the cost. This is not speedy, and you may find it necessary to eventually code the whole analysis in Matlab.

function main

examples of reading

xlsread('example.xlsx','sheet1','b1')
xlsread('example.xlsx','sheet1','b2')

xlswrite('example.xlsx',4,'sheet1','b1')

ans =

     3


ans =

     8

xlsread('example.xlsx','sheet1','b1')
xlsread('example.xlsx','sheet1','b2')
% you can see we did set the value of b1 as we said, and the value of b2 is
% updated also.

ans =

     4


ans =

    15

Find roots

there are two solutions, . We try guesses above and below each one.

positive root

fsolve(@f,2)
fsolve(@f,0.8)

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

    1.0000


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

    1.0000

negative root

fsolve(@f,-2)
fsolve(@f,-0.8)
% note it is not fast to solve this!

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

   -1.0000


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

   -1.0000

make a plot

x = linspace(-2,2,10);
y = arrayfun(@f,x); %this maps the function f onto the vector x

plot(x,y)
% note that this is also pretty slow.

function y = f(x)
xlswrite('example.xlsx',x,'sheet1','b1');
y = xlsread('example.xlsx','sheet1','b2');

% categories: File IO

% post_id = 739; %delete this line to force new post;

Published with MATLAB® 7.10