compute pipe diameter

October 27, 2011 at 07:26 PM | categories: nonlinear algebra | View Comments

compute pipe diameter

compute pipe diameter

A heat exchanger must handle 2.5 L/s of water through a smooth pipe with length of 100 m. The pressure drop cannot exceed 103 kPa at 25 degC. Compute the minimum pipe diameter required for this application.

Adapted from problem 8.8 in Problem solving in chemical and Biochemical Engineering with Polymath, Excel, and Matlab. page 303.

Contents

Solution

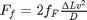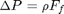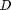We need to estimate the Fanning friction factor for these conditions so we can estimate the frictional losses that result in a pressure drop for a uniform, circular pipe. The frictional forces are given by $F_f = 2f_F \frac{\Delta L v^2}{D}$, and the corresponding pressure drop is given by $\Delta P = \rho F_f$. In these equations, $\rho$ is the fluid density, $v$ is the fluid velocity, $D$ is the pipe diameter, and 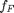$f_F$ is the Fanning friction factor. 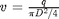The average fluid velocity is given by $v = \frac{q}{\pi D^2/4}$.

For laminar flow, we estimate 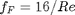$f_F = 16/Re$, which is a linear equation, and for turbulent flow (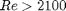$Re > 2100$) we have the implicit equation 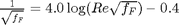$\frac{1}{\sqrt{f_F}}=4.0 \log(Re \sqrt{f_F})-0.4$. Of course, we define 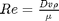$Re = \frac{D v\rho}{\mu}$ where $\mu$ is the viscosity of the fluid.

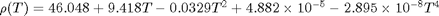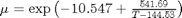It is known that $\rho(T) = 46.048 + 9.418 T -0.0329 T^2 +4.882\times10^{-5}-2.895\times10^{-8}T^4$ and $\mu = \exp\left({-10.547 + \frac{541.69}{T-144.53}}\right)$ where $\rho$ is in kg/m^3 and $\mu$ is in kg/(m*s).

function main

clear all; close all

u = cmu.units;

T = u.degC(25);
Q = 2.5*u.L/u.s;
deltaP = 103*u.kPa;
deltaL = 100*u.m;

% Note these correlations expect dimensionless T, where the magnitude
% of T is in K
rho = @(T) (46.048 + 9.418*T -0.0329*T^2 +4.882e-5*T^3-2.895e-8*T^4)*u.kg/u.m^3;
mu = @(T) exp(-10.547 + 541.69/(T-144.53))*u.Pa*u.s;

    function fF = fanning_friction_factor(Re)
        if Re < 2100
            error('Flow is probably not turbulent')
        end
        % solve the Nikuradse correlation to get the friction factor
        fz = @(f) 1/sqrt(f) - (4.0*log10(Re*sqrt(f))-0.4);
        fF = fzero(fz, 0.01);
    end

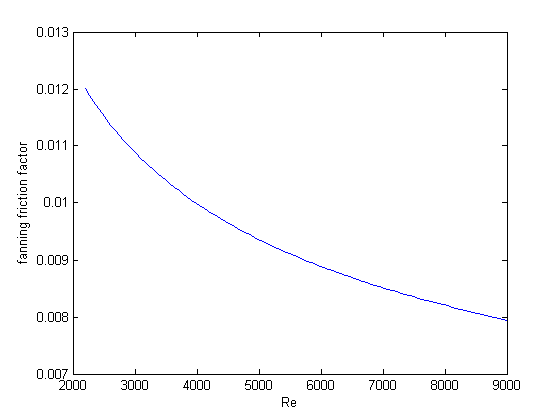
plot fanning friction factor

Re = linspace(2200,9000);
f = arrayfun(@fanning_friction_factor,Re);
plot(Re,f)
xlabel('Re')
ylabel('fanning friction factor')
% You can see why we use 0.01 as an initial guess for solving for the
% Fanning friction factor; it falls in the middle of ranges possible
% for these Re numbers.

Solve the problem

The aim is to find 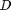$D$ that solves: $ \Delta p = \rho 2 f_F \frac{\Delta L v^2}{D}$. This is a nonlinear equation in 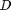$D$, since D affects the fluid velocity, the Re, and the Fanning friction factor. Here is the function that we need to solve:

    function z = objective(D)
        v = Q/(pi*D^2/4);
        Re = D*v*rho(double(T))/mu(double(T));

        fF = fanning_friction_factor(Re);

        z = deltaP - 2*fF*rho(double(T))*deltaL*v^2/D;
    end

D = fzero(@objective,0.04*u.m)
fprintf('The minimum pipe diameter is %s\n', D.as(u.mm,'%1.2f'))

0.0389653*m
The minimum pipe diameter is 38.97*mm

Any pipe diameter smaller than that value will result in a larger pressure drop at the same volumetric flow rate, or a smaller volumetric flowrate at the same pressure drop. Either way, it will not meet the design specification.

Notes:

If D happened to be large enough to result in laminar flow, this solution would break down, because we didn't define a fanning friction factor correlation for laminar flow. We could do that in our fanning friction factor function, but some care should be taken to ensure it is continuous.

end % main

% categories: Nonlinear algebra
% tags: fluids


Published with MATLAB® 7.13

blog comments powered by Disqus