Phase portraits of a system of ODEs
August 09, 2011 at 03:54 PM | categories: odes | View Comments
Contents
Phase portraits of a system of ODEs
adapted from http://www-users.math.umd.edu/~tvp/246/matlabode2.html
clear all; close all; clc
Problem setup
An undamped pendulum with no driving force is described by
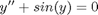
We reduce this to standard matlab form of a system of first order ODEs by letting  and
and 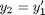 . This leads to:
. This leads to:
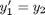

The phase portrait is a plot of a vector field which qualitatively shows how the solutions to these equations will go from a given starting point. here is our definition of the differential equations:
f = @(t,Y) [Y(2); -sin(Y(1))];
To generate the phase portrait, we need to compute the derivatives 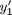 and
and 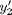 at
at  on a grid over the range of values for
on a grid over the range of values for 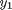 and
and 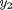 we are interested in. We will plot the derivatives as a vector at each (y1, y2) which will show us the initial direction from each point. We will examine the solutions over the range -2 < y1 < 8, and -2 < y2 < 2 for y2, and create a grid of 20x20 points.
we are interested in. We will plot the derivatives as a vector at each (y1, y2) which will show us the initial direction from each point. We will examine the solutions over the range -2 < y1 < 8, and -2 < y2 < 2 for y2, and create a grid of 20x20 points.
y1 = linspace(-2,8,20); y2 = linspace(-2,2,20); % creates two matrices one for all the x-values on the grid, and one for % all the y-values on the grid. Note that x and y are matrices of the same % size and shape, in this case 20 rows and 20 columns [x,y] = meshgrid(y1,y2); size(x) size(y)
ans =
20 20
ans =
20 20
computing the vector field
we need to generate two matrices, u and v. u will contain the value of y1' at each x and y position, while v will contain the value of y2' at each x and y position of our grid.
we preallocate the arrays so they have the right size and shape
u = zeros(size(x)); v = zeros(size(x)); % we can use a single loop over each element to compute the derivatives at % each point (y1, y2) t=0; % we want the derivatives at each point at t=0, i.e. the starting time for i = 1:numel(x) Yprime = f(t,[x(i); y(i)]); u(i) = Yprime(1); v(i) = Yprime(2); end
now we use the quiver command to plot our vector field
quiver(x,y,u,v,'r'); figure(gcf) xlabel('y_1') ylabel('y_2') axis tight equal;
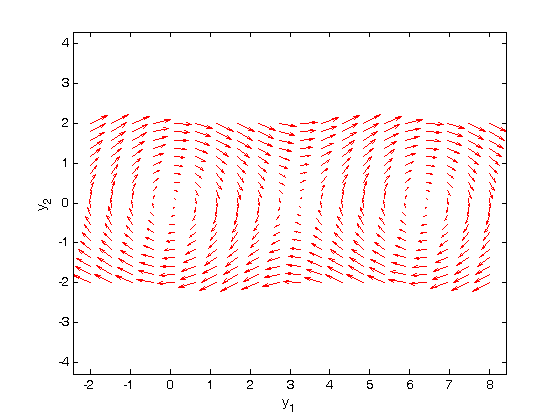
Plotting solutions on the vector field
Let's plot a few solutions on the vector field. We will consider the solutions where y1(0)=0, and values of y2(0) = [0 0.5 1 1.5 2 2.5], in otherwords we start the pendulum at an angle of zero, with some angular velocity.
hold on for y20 = [0 0.5 1 1.5 2 2.5] [ts,ys] = ode45(f,[0,50],[0;y20]); plot(ys(:,1),ys(:,2)) plot(ys(1,1),ys(1,2),'bo') % starting point plot(ys(end,1),ys(end,2),'ks') % ending point end hold off
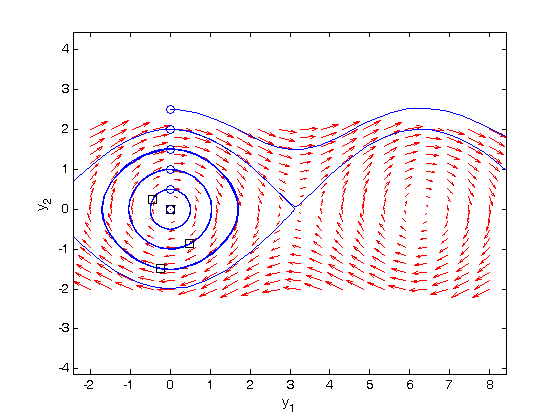
what do these figures mean? For starting points near the origin, and small velocities, the pendulum goes into a stable limit cycle. For others, the trajectory appears to fly off into y1 space. Recall that y1 is an angle that has values from  to
to  . The y1 data in this case is not wrapped around to be in this range.
. The y1 data in this case is not wrapped around to be in this range.
'done' % categories: ODEs % tags: math % post_id = 799; %delete this line to force new post;
ans = done