Symbolic math in Matlab
August 10, 2011 at 04:16 PM | categories: symbolic | View Comments
Symbolic math in Matlab
Matlab has some capability to perform symbolic math.
Contents
Solve the quadratic equation
syms a b c x % this declares a b c and x to be symbolic variables f = a*x^2 + b*x + c solution = solve(f,x)
f = a*x^2 + b*x + c solution = -(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a)
the solution you should recognize in the form of 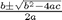 although Matlab does not print it this nicely!
although Matlab does not print it this nicely!
pretty(solution) % this does a slightly better ascii art rendition
+- -+ | 2 1/2 | | b + (b - 4 a c) | | - ------------------- | | 2 a | | | | 2 1/2 | | b - (b - 4 a c) | | - ------------------- | | 2 a | +- -+
differentiation
you might find this helpful!
diff(f) % first derivative diff(f,2) % second derivative
ans = b + 2*a*x ans = 2*a
diff(f,a) % derivative of f with respect to a
ans = x^2
integration
int(f)
int(f, 0, 1) % definite integral from 0 to 1
ans = (a*x^3)/3 + (b*x^2)/2 + c*x ans = a/3 + b/2 + c
Analytically solve a simple ODE
ode = 'Dy = y'; % note the syntax: Dy = dydx init = 'y(0)=1'; independent_variable = 'x'; y = dsolve(ode, init, independent_variable)
y = exp(x)
evaluate the solution at a few places
say x=4 using the subs command.
subs(y,4)
ans = 54.5982
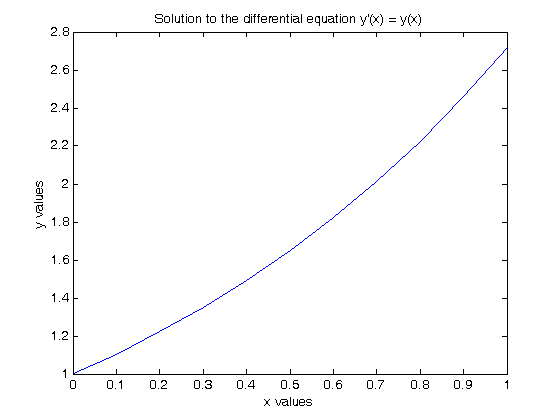
we can also evaluate it on a range of values, say from 0 to 1.
x = 0:0.1:1; Y = subs(y,x); plot(x,Y) xlabel('x values') ylabel('y values') title('Solution to the differential equation y''(x) = y(x)')
Warning! this note is in the dsolve documentation
Note By default, the solver does not guarantee general correctness and completeness of the results. If you do not set the option IgnoreAnalyticConstraints to none, always verify results returned by the dsolve command.
Let's see what this means
y1 = dsolve('Dy=1+y^2','y(0)=1') y2 = dsolve('Dy=1+y^2','y(0)=1',... 'IgnoreAnalyticConstraints','none')
y1 = tan(pi/4 + t) y2 = piecewise([C13 in Z_, tan(pi/4 + t + pi*C13)])
those solutions look different, but it isn't clear what do to with the second one.
see also: http://www.cs.utah.edu/~germain/PPS/Topics/Matlab/symbolic_math.html and http://www.mathworks.com/help/toolbox/symbolic/brvfu8o-1.html
% categories: Symbolic % tags: math