Matlab meets the steam tables

John Kitchin

A Matlab module for the steam tables is available for download at http://www.x-eng.com/XSteam_Matlab.htm. To do this example yourself, you need to download this zipfile and unzip it into your Matlab path. Today we will examine using this module for examining the Rankine power generation cycle, following example3.7-1 in Sandler's Thermodynamics book.

Problem statement: A Rankine cycle operates using steam with the condenser at 100 degC, a pressure of 3.0 MPa and temperature of 600 degC in the boiler. Assuming the compressor and turbine operate reversibly, estimate the efficiency of the cycle.

We will use the XSteam module to compute the required properties. There is only one function in XSteam, which takes a string and one or two arguments. The string specifies which subfunction to use.

We will use these functions from the module.

Contents

psat_T Saturation pressure (bar) at a specific T in degC
sL_T   Entropy (kJ/kg/K) of saturated liquid at T(degC)
hL_T   Enthalpy (kJ/kg)of saturated liquid at T(degC)
vL_T   Saturated liquid volume (m^3/kg)
T_ps   steam Temperature (degC) for a given pressure (bar) and entropy (kJ/kg/K)
h_pt   steam enthalpy (kJ/kg) at a given pressure (bar) and temperature (degC)
s_pt   steam entropy (kJ/kg/K) at a given pressure (bar) and temperature (degC)

We will use the cmu.units package to keep track of the units. Remember that the units package internally stores units in terms of base units, so to get a pressure in bar, we use the syntax P/u.bar, which is a dimensionless number with a magnitude equal to the number of bar.

clear all; clc; close all
u = cmu.units;

Starting point in the Rankine cycle in condenser.

we have saturated liquid here, and we get the thermodynamic properties for the given temperature.

T1 = 100; % degC
P1 = XSteam('psat_T',T1)*u.bar;
s1 = XSteam('sL_T', T1)*u.kJ/u.kg/u.K;
h1 = XSteam('hL_t', T1)*u.kJ/u.kg;
v1 = XSteam('vL_T', T1)*u.m^3/u.kg; % we need this to compute compressor work

isentropic compression of liquid to point 2

The final pressure is given, and we need to compute the new temperatures, and enthalpy.

P2 = 3*u.MPa;
s2 = s1;  % this is what isentropic means
T2 = XSteam('T_ps',P2/u.bar, s1/(u.kJ/u.kg/u.K));
h2 = XSteam('h_pt', P2/u.bar,T2)*u.kJ/u.kg;

% work done to compress liquid. This is an approximation, since the
% volume does change a little with pressure, but the overall work here
% is pretty small so we neglect the volume change.
WdotP = v1*(P2-P1);
fprintf('the compressor work is: %s\n', WdotP.as(u.kJ/u.kg,'%1.2f'))

the compressor work is: 3.02*kJ/kg

isobaric heating to T3 in Boiler where we make steam

T3 = 600; % degC
P3 = P2; % this is what isobaric means
h3 = XSteam('h_pt', P3/u.bar, T3)*u.kJ/u.kg;
s3 = XSteam('s_pt', P3/u.bar, T3)*u.kJ/u.kg/u.K;

Qb = h3 - h2; % heat required to make the steam
fprintf('the boiler heat duty is: %s\n', Qb.as(u.kJ/u.kg,'%1.2f'))

the boiler heat duty is: 3260.68*kJ/kg

isentropic expansion through turbine to point 4

Still steam

T4 = XSteam('T_ps',P1/u.bar, s3/(u.kJ/u.kg/u.K));
h4 = XSteam('h_pt', P1/u.bar, T4)*u.kJ/u.kg;
s4 = s3; % isentropic
Qc = h4 - h1; % work required to cool from T4 to T1 in the condenser
fprintf('the condenser heat duty is: %s\n', Qc.as(u.kJ/u.kg,'%1.2f'))

the condenser heat duty is: 2316.99*kJ/kg

This heat flow is not counted against the overall efficiency. Presumably a heat exchanger can do this cooling against the cooler environment, so only heat exchange fluid pumping costs would be incurred.

to get from point 4 to point 1

WdotTurbine = h4 - h3; % work extracted from the expansion
fprintf('the turbine work is: %s\n', WdotTurbine.as(u.kJ/u.kg,'%1.2f'))

the turbine work is: -946.72*kJ/kg

efficiency

This is a ratio of the work put in to make the steam, and the net work obtained from the turbine. The answer here agrees with the efficiency calculated in Sandler on page 135.

eta = -(WdotTurbine - WdotP)/Qb

fprintf('the overall efficiency is %1.0f%%\n', (eta*100))

eta =

   0.291271696419079

the overall efficiency is 29%

Entropy-temperature chart

The XSteam module makes it pretty easy to generate figures of the steam tables. Here we generate an entropy-Temperature graph.

T = linspace(0,800,200); % range of temperatures

figure; hold on
% we need to compute S-T for a range of pressures. Here
for P = [0.01 0.1 1 5 30 100 250 500 1000] % bar
    % XSteam is not vectorized, so here is an easy way to compute a
    % vector of entropies
    S = arrayfun(@(t) XSteam('s_PT',P,t),T);
    plot(S,T,'k-')
    text(S(end),T(end),sprintf('%1.1f bar',P),'rotation',90)
end
set(gca,'Position',[0.13 0.11 0.775 0.7])

% saturated vapor and liquid entropy lines
svap = arrayfun(@(t) XSteam('sV_T',t),T);
sliq = arrayfun(@(t) XSteam('sL_T',t),T);

plot(svap,T,'r-')
plot(sliq,T,'b-')
xlabel('Entropy (kJ/(kg K)')
ylabel('Temperature (^\circC)')

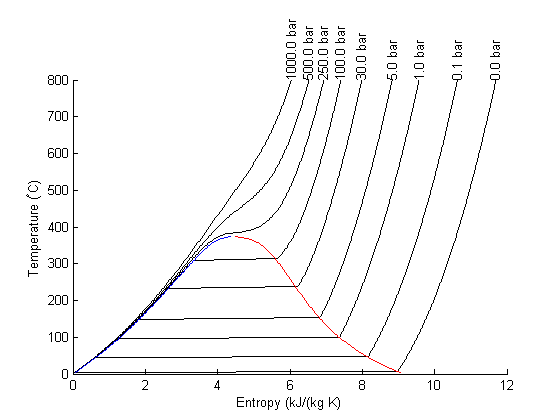
Plot Path

The path from 1 to 2 is isentropic, and has a small T change.

plot([s1 s2]/(u.kJ/u.kg/u.K),...
    [T1 T2],'ro ','markersize',8,'markerfacecolor','r')

% the path from 2 to 3 is isobaric
T23 = linspace(T2, T3);
S23 = arrayfun(@(t) XSteam('s_PT',P2/u.bar,t),T23);
plot(S23,T23,'b-','linewidth',4)

% the path from 3 to 4 is isentropic
plot([s3 s4]/(u.kJ/u.kg/u.K),...
    [T3 T4],'g-','linewidth',4)

% and from 4 to 1 is isobaric
T41 = linspace(T4,T1-0.01); % subtract 0.01 to get the liquid entropy
S41 = arrayfun(@(t) XSteam('s_PT',P1/u.bar,t),T41);
plot(S41,T41,'r-','linewidth',4)

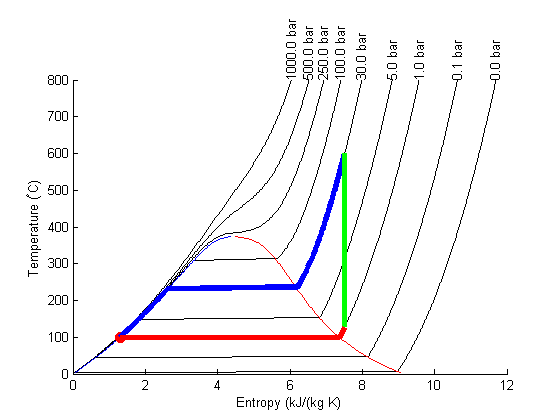
Note steps 1 and 2 are very close together on this graph and hard to see.

Summary

This was an interesting exercise. On one hand, the tedium of interpolating the steam tables is gone. On the other hand, you still have to know exactly what to ask for to get an answer that is correct. The XSteam interface is a little clunky, and takes some getting used to. It would be nice if it was vectorized to avoid the arrayfun calls.

% categories: Miscellaneous
% tags: Thermodynamics

Published with MATLAB® 7.13