The trapezoidal method of integration
October 15, 2011 at 12:44 AM | categories: basic matlab | View Comments
Contents
The trapezoidal method of integration
John Kitchin
See http://en.wikipedia.org/wiki/Trapezoidal_rule
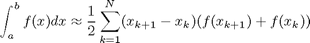
Let's compute the integral of sin(x) from x=0 to 
. To approximate the integral, we need to divide the interval from 
to 
into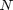 
intervals. The analytical answer is 2.0.
We will use this example to illustrate the difference in performance between loops and vectorized operations in Matlab.
a = 0; b = pi; N = 1000; % this is the number of intervals h = (b - a)/N; % this is the width of each interval x = a:h:b; % note there are N+1 elements in this x vector y = sin(x); % the sin function is already vectorized, so y contains N+1 elements
Trapezoid method using a loop
we use the tic and toc functions to time how long it takes to run.
tic f = 0; for k=1:N f = f + 0.5*((x(k+1)-x(k))*(y(k+1)+y(k))); end f toc
f =
2.0000
Elapsed time is 0.002520 seconds.
vectorized approach
tic Xk = x(2:end)-x(1:end-1); % vectorized version of (x(k+1)-x(k)) Yk = y(2:end)+y(1:end-1); % vectorized version of (y(k+1)+y(k)) f = 0.5*sum(Xk.*Yk) % vectorized version of the loop above toc % It isn't strictly necessary to calculate Xk this way, since here by % design every interval is the same width, but this approach would work for % non-uniform x-values.
f =
2.0000
Elapsed time is 0.000148 seconds.
total linear algebra way
In the last example, there may be loop buried in the sum command. Lets do one final method, using linear algebra, in a single line. The key to understanding this is to recognize the sum is just the result of a dot product of the x differences and y sums. We have to transpose the y sums to get the vector dimensions to work for the dot product (* is matrix multiplication/dot product in Matlab
tic f = 0.5*(x(2:end)-x(1:end-1))*(y(2:end)+y(1:end-1))' toc
f =
2.0000
Elapsed time is 0.000130 seconds.
summary
The loop method is straightforward to code, and looks alot like the formula that defines the trapezoid method. the vectorized methods are not as easy to read, and take fewer lines of code to write. However, the vectorized methods are much faster than the loop, so the loss of readability could be worth it for very large problems.
% categories: basic matlab % tags: math % post_id = 1231; %delete this line to force new post; % permaLink = http://matlab.cheme.cmu.edu/2011/10/14/the-trapezoidal-method-of-integration/;