Matlab in Chemical Engineering at CMU

solving a second order ode

September 26, 2011 at 11:02 PM | categories: odes | View Comments

solving a second order ode

the Van der Pol oscillator Matlab can only solve first order ODEs, or systems of first order ODES. To solve a second order ODE, we must convert it by changes of variables to a system of first order ODES. We consider the Van der Pol oscillator here:

phase portrait

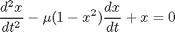
$\frac{d^2x}{dt^2} - \mu(1-x^2)\frac{dx}{dt} + x = 0$

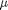$\mu$ is a constant. If we let 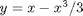$y=x - x^3/3$ http://en.wikipedia.org/wiki/Van_der_Pol_oscillator, then we arrive at this set of equations:

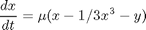
$\frac{dx}{dt} = \mu(x-1/3x^3-y)$

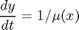
$\frac{dy}{dt} = 1/\mu(x)$

here is how we solve this set of equations. Let 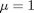$\mu=1$ .

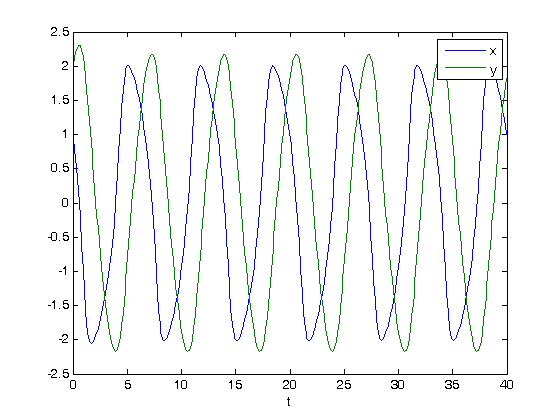
function main

X0 = [1;2];
tspan = [0 40];
[t,X] = ode45(@VanderPol, tspan, X0);

x = X(:,1);
y = X(:,2);

plot(t,x,t,y)
xlabel('t')
legend 'x' 'y'

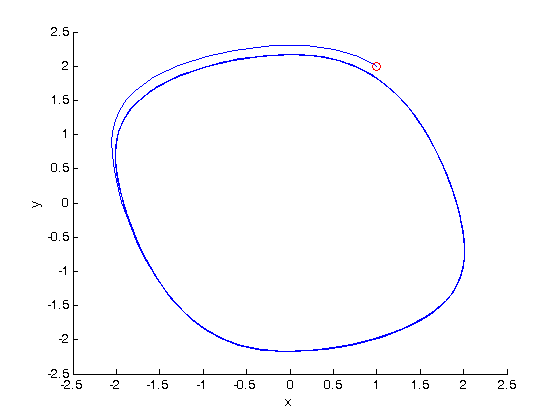
phase portrait

it is common to create a phase portrait. Although the solution appears periodic above, here you can see a limit cycle is definitely approached after the initial transient behavior. We mark the starting point with a red circle.

figure
hold on
plot(x,y)
plot(x(1),y(1),'ro') % starting point for reference
xlabel('x')
ylabel('y')

'done'

ans =

done

function dXdt = VanderPol(t,X)
x = X(1);
y = X(2);
mu = 1;
dxdt = mu*(x-1/3*x^3-y);
dydt = x/mu;
dXdt = [dxdt; dydt];

% categories: ODEs
% tags: math

solving a second order ode

Contents

phase portrait