Solving integral equations

John Kitchin

Contents

Occasionally we have integral equations we need to solve in engineering problems, for example, the volume of plug flow reactor can be defined by this equation: where 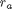is the rate law. Suppose we know the reactor volume is 100 L, the inlet molar flow of A is 1 mol/L, the volumetric flow is 10 L/min, and , with 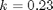1/min. What is the exit molar flow rate? We need to solve the following equation:

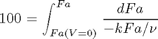
k = 0.23;
nu = 10;
Fao = 1;

We start by creating a function handle that describes the integrand. We can use this function in the quad command to evaluate the integral.

f1 = @(Fa) -1./(k*Fa/nu);

Now we create a second function handle that defines the equation to solve. We use the integrand function handle above in the quad command to evaluate the integral

f2 = @(Fa) 100 - quad(f1,Fao,Fa);

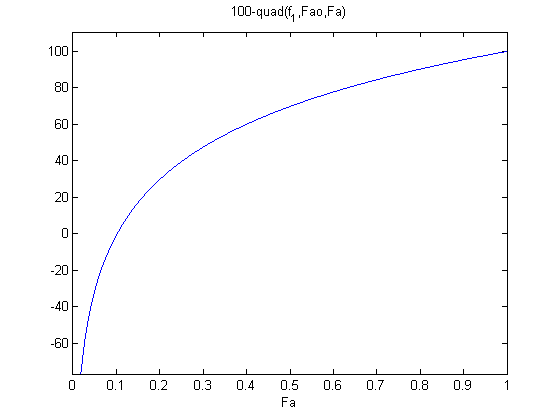
plot f2 to get an idea of where the solution is.

the maximum that Fa can be is Fao, and the minimum is zero. From the graph you can see the solution is at approximately Fa = 0.1.

ezplot(f2,0,Fao)

Warning: Function failed to evaluate on array inputs; vectorizing the function may
speed up its evaluation and avoid the need to loop over array elements. 

Get the solution

Fa_guess = 0.1;
Fa_exit = fsolve(f2, Fa_guess);

Ca_exit = Fa_exit/nu;
sprintf('The exit concentration is %1.2f mol/L',Ca_exit)

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

The exit concentration is 0.01 mol/L

% categories: nonlinear algebra
% tags: reaction engineering
% post_id = 954; %delete this line to force new post;

Published with MATLAB® 7.12