Integrating functions in Matlab
August 01, 2011 at 06:12 PM | categories: basic matlab | View Comments
Contents
Integrating functions in Matlab
it is a good idea to add these lines to the top of your m-files. They keep things looking neat!
close all % close all figure windows that are open clear all % clear all the variables currently stored in memory clc % clear the commands in the command window
Problem statement
find the integral of a function f(x) from a to b i.e.
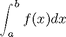
In matlab we use numerical quadrature to achieve this with the `quad` command. f = @(x) some_function_of_x quad(f,a,b)
as a specific example, lets integrate
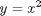
from x=0 to x=1. You should be able to work out that the answer is 1/3.
f = @(x) x.^2; %note we must use .^ to ensure element-wise squaring
a = 0;
b = 1;
integrand = quad(f,a,b)
integrand =
0.3333
double integrals
we use the `dblquad` command
Integrate 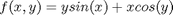 over
over
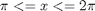
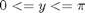
i.e.
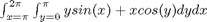
f = @(x,y) y*sin(x)+x*cos(y); x1=pi; x2=2*pi; y1=0; y2=pi; integrand = dblquad(f, x1,x2,y1,y2)
integrand = -9.8696
triple integrals
we use the `triplequad` command Integrate 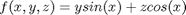 over the region
over the region
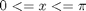
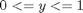
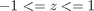
f = @(x,y,z) y*sin(x)+z*cos(x); x1=0; x2=pi; y1=0; y2=1; z1=-1; z2=1; integrand = triplequad(f, x1,x2,y2,y2,z1,z2) % categories: Basic matlab % tags: math
integrand =
0