Linear least squares fitting with linear algebra

John Kitchin

clear all; clc; close all
% Given this data, we want to fit a line to the data to extract the slope.
u = cmu.units;
x = [0 0.5 1 1.5 2 3 4 6 10]*u.s;  % time
y = [0 -0.157 -0.315 -0.472 -0.629 -0.942 -1.255 -1.884 -3.147]*u.dimensionless; % dimensionless

figure
plot(x,y,'bo ')

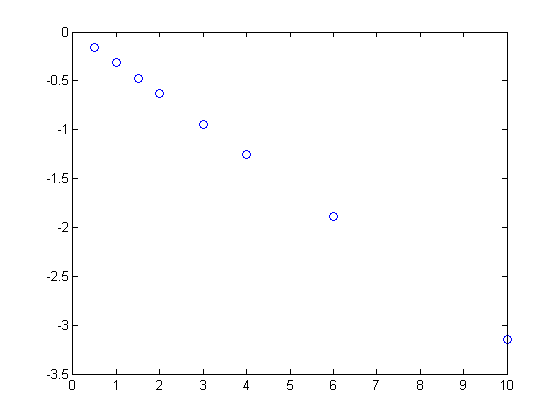
The nature of this method is that we can write a series of equations:

x1^0*b0 + x1*b1 = y1
x2^0*b0 + x2*b1 = y2
x3^0*b0 + x3*b1 = y3
etc...

Which we can write in matrix form: X b = y.

where X is a matrix of column vectors like this:

X = [(x.^0)' x']

matrix with mixed row or column units

ans =

    1.0000         0
    1.0000    0.5000
    1.0000    1.0000
    1.0000    1.5000
    1.0000    2.0000
    1.0000    3.0000
    1.0000    4.0000
    1.0000    6.0000
    1.0000   10.0000

We cannot solve for the unknowns b, because the X matrix is not square. There are many more rows in X than in B. to make X square, we left multiply each side by transpose(X) to get

X^T X b = X^T y

then we can use the Matlab syntax with the backslash operator that solves linear equations

b = (X'*X)\(X'*y')
b2 = b(2)

|0.00|
-0.31|
-0.314522

or even more directly, since the backslash operator solves in the least squares sense if there are more rows than columns. Note these only work for linear equations!

b = X\y'
b2 = b(2)

matrix with mixed row or column units

ans =

    0.0006
   -0.3145

-0.314522/s

the intercept is b(1), and the slope is b(2). We can make a simple function of the fit, and plot it on the data.

fit = @(z) b(1) + b(2)*z;
hold all
h = plot(x, X*b, 'r- ');

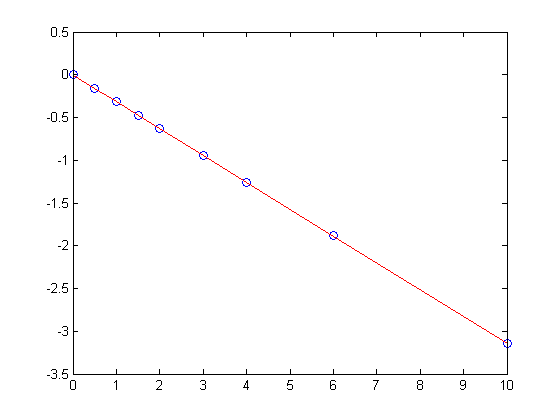
this method can be readily extended to fitting any polynomial model, or other linear model that is fit in a least squares sense. This method does not provide confidence intervals, as the related method discussed in Post 943 using the regress command, but it is probably how that method does the fitting.

'done'

% categories: data analysis
% post_id = 1141; %delete this line to force new post;

ans =

done

Published with MATLAB® 7.12