Matlab in Chemical Engineering at CMU

Contents

Another way to parameterize an ODE - nested function

John Kitchin

In Post 1108 we saw one method to parameterize an ODE, by creating an ode function that takes an extra parameter argument, and then making a function handle that has the syntax required for the solver, and passes the parameter the ode function.

The problem with passing a parameter to a subfunction is that each function maintains a separate namespace, so each function cannot see the variables in another function. One way to address that in matlab is to use a nested function, or a function inside a function.

In the code template below, this is a function/subfunction.

function main
code....
% comment
function dxdt=myode(t,x)
code ...

In these kinds of definitions, each function implicitly ends when a new line with a function is defined.

In a nested function we have this syntax:

 function main
 code
 % comment
     function dxdt=nestedode(t,x)
        code
     end
 code
 end

Since the nested function is in the namespace of the main function, it can "see" the values of the variables in the main function.

We will use this method to look at teh solution to the van der Pol equation for several different values of mu.

function main

clear all; close all; clc
figure
hold all

for mu = [0.1 1 2 5]
    tspan = [0 100];
    X0 = [0 3];
    [t,X] = ode45(@myode,tspan,X0);
    x = X(:,1); y = X(:,2);
    plot(x,y,'DisplayName',sprintf('mu = %1.0f',mu))
end
axis equal
legend('-DynamicLegend','location','best')

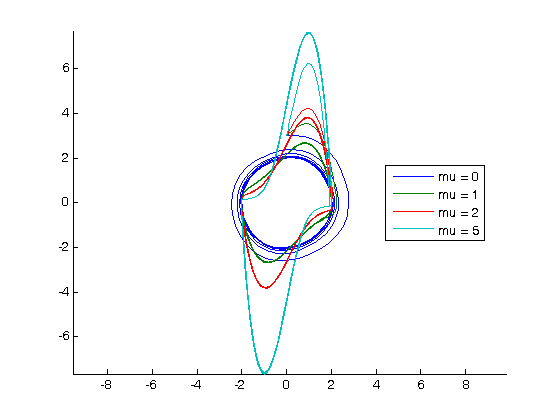
You can see the solution changes dramatically for different values of mu. The point here isn't to understand why, but to show an easy way to study a parameterize ode with a nested function.

Note the nested function is indented. That is for readability. This function uses the mu value defined in the main function.

    function dXdt = myode(t,X)
        % van der Pol equations
        x = X(1);
        y = X(2);

        dxdt = y;
        dydt = -x+mu*(1-x^2)*y;

        dXdt = [dxdt; dydt];

    end

Summary

Nested functions can be a great way to "share" variables between functions especially for ODE solving, and nonlinear algebra solving, or any other application where you need a lot of parameters defined in one function in another function.

end

% categories: odes
% tags: math

% post_id = 1130; %delete this line to force new post;

Published with MATLAB® 7.12