finding minima and maxima in ODE solutions with events

John Kitchin

Today we look at another way to use events in an ode solver. We use an events function to find minima and maxima, by evaluating the ODE in the event function to find conditions where the first derivative is zero, and approached from the right direction.

We use a simple ODE, y' = sin(x)*e^-0.05x, which has minima and maxima.

function main

clear all; close all;

y0 = 0;
options = odeset('Events',@events)
[t,y,te,ye,ie] = ode45(@myode, [0 20],y0,options);

plot(t,y,'r-')

options = 

              AbsTol: []
                 BDF: []
              Events: @events
         InitialStep: []
            Jacobian: []
           JConstant: []
            JPattern: []
                Mass: []
        MassConstant: []
        MassSingular: []
            MaxOrder: []
             MaxStep: []
         NonNegative: []
         NormControl: []
           OutputFcn: []
           OutputSel: []
              Refine: []
              RelTol: []
               Stats: []
          Vectorized: []
    MStateDependence: []
           MvPattern: []
        InitialSlope: []

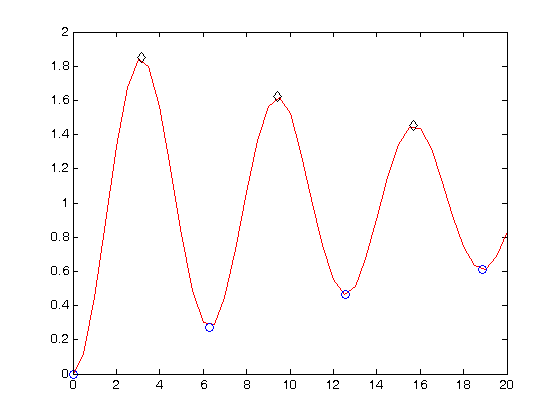
Put a blue circle at the minima the minima correspond to event 1, and the maxima to event 2, according to to our events function.

hold all
plot(te(ie==1),ye(ie==1),'bo ')
% Put a black diamond at the maxima
plot(te(ie==2),ye(ie==2),'kd ')

'done'

ans =

done

Events are powerful ways to interact with your ODE solutions. See also event finding, advanced event finding.

function dydx = myode(x,y)
% nothing fancy here. just an oscillating function.
dydx = sin(x)*exp(-0.05*x);

function [value,isterminal,direction] = events(x,y)
% we define two events.
% at minimum, dydx = 0, direction = 1 event function is increasing after
% the minimum.
%
% at maximum, dydx = 0, direction = -1 event function is decreasing after
% the maximum
%
% We create a vector for each output.
value = [myode(x,y) myode(x,y)]; % this is the derivative
isterminal = [0 0];   % do not stop the integration
direction = [1 -1];

% categories: ODEs

Published with MATLAB® 7.10