Parameterized ODEs

John Kitchin

Sometimes we have an ODE that depends on a parameter, and we want to solve the ODE for several parameter values. It is inconvenient to write an ode function for each parameter case. Here we examine a convenient way to solve this problem. We consider the following ODE:

Contents

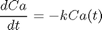
where is a parameter, and we want to solve the equation for a couple of values of to test the sensitivity of the solution on the parameter. Our question is, given 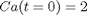, how long does it take to get 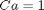, and how sensitive is the answer to small variations in ?

function main

clear all; close all; clc
ko = 2;
tspan = [0 1]; % you need to make sure this time span contains the solution!
Cao = 2;

finding the solution

we will use an events function to make the integration stop where we want it to. First we create an options variable for our ode solver to use the event function to stop integrating at Ca = 1

options = odeset('Events',@event_function);

we will look at +- 5% of the given k-value

ktest = [0.95*ko ko 1.05*ko]
results = [];

ktest =

    1.9000    2.0000    2.1000

this syntax loops through each value in ktest, setting the kvar variable equal to that value inside the loop.

for kvar = ktest
    % make a function handle using the k for this iteration
    f = @(t,Ca) myode(t,Ca,kvar);
    [t,Ca,TE,VE] = ode45(f, tspan, Cao,options);
    % TE is the time at which Ca = 1
    results = [results TE] % store time for later analysis
    plot(t,Ca,'displayname',sprintf('k = %1.2f',kvar))
    hold all
end

legend('-DynamicLegend')
xlabel('Time')
ylabel('C_A')

results =

    0.3648


results =

    0.3648    0.3466


results =

    0.3648    0.3466    0.3301

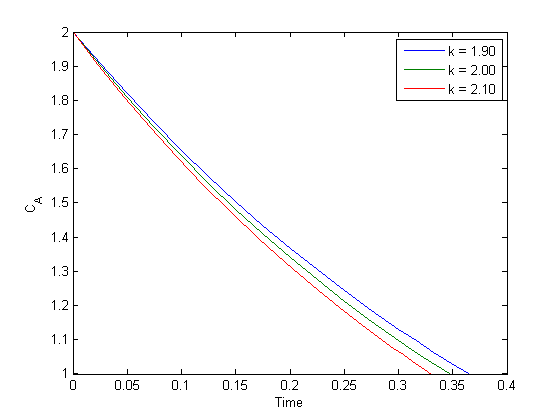
sprintf('k = %1.2f:  Ca = 1 at %1.2f time units\n',[ktest;results])

ans =

k = 1.90:  Ca = 1 at 0.36 time units
k = 2.00:  Ca = 1 at 0.35 time units
k = 2.10:  Ca = 1 at 0.33 time units

compute errors

we can compute a percent difference for each variation. We assume that ko is the reference point

em = (results(1) - results(2))/results(2)*100
ep = (results(3) - results(2))/results(2)*100
% We see roughly +-5% error for a 5% variation in the parameter. You
% would have to apply some engineering judgement to determine if that
% is sufficiently accurate.

em =

    5.2632


ep =

   -4.7619

function dCadt = myode(t,Ca,k)
dCadt = -k*Ca;

function [value,isterminal,direction] = event_function(t,Ca)
value = Ca - 1.0;  % when value = 0, an event is triggered
isterminal = 1; % terminate after the first event
direction = 0;  % get all the zeros

% categories: ODEs
% tags: reaction engineering

Published with MATLAB® 7.12