Matlab in Chemical Engineering at CMU

Contents

On the quad, or trapz'd in ChemE heaven?

John Kitchin

What is the difference between quad and trapz? The short answer is that quad integrates functions (via a function handle) using numerical quadrature, and trapz performs integration of arrays of data using the trapezoid method.

Let's look at some examples. We consider the example of computing 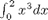. the analytical integral is 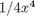, so we know the integral evaluates to 16/4 = 4. This will be our benchmark for comparison to the numerical methods.

clear all; clc; close all;

quad usage

This command is equivalent to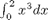

i1 = quad(@(x) x.^3,0,2)

i1 =

     4

we can also define the function handle separately.

f = @(x) x.^3
f(2) % should be 8

f = 

    @(x)x.^3


ans =

     8

This command is equivalent to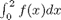

i1 = quad(f,0,2)
error = (i1 - 4)/4
% Note the error is very small!

i1 =

     4


error =

     0

Trapz usage

if we had numerical data like this, we use trapz to integrate it

x = [0 0.5 1 1.5 2];
y = f(x);  % or you could say y = x.^3

i2 = trapz(x,y)
error = (i2 - 4)/4

i2 =

    4.2500


error =

    0.0625

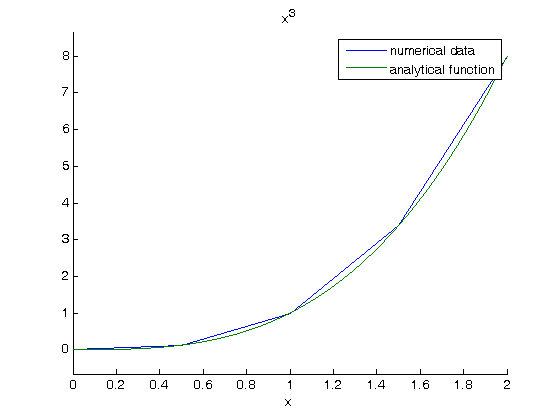
Note the integral of these vectors is greater than 4! You can see why here.

figure; hold all
plot(x,y)
ezplot(f,[0 2])
legend 'numerical data' 'analytical function'
% The area of the trapezoids is greater than the area under the function
% due to the coarse sampling of $f(x)=x^3$.

with a finer sampling we have:

x = linspace(0,2); % 100 points between 0, 1
y = x.^3;
i3 = trapz(x,y)

i3 =

    4.0004

and a much smaller error.

error = (i3 - 4)/4

error =

  1.0203e-004

Combining numerical data with quad

You might want to combine numerical data with the quad function if you want to perform integrals easily. Let's say you are given this data:

x = [0 0.5 1 1.5 2];
y = [0    0.1250    1.0000    3.3750    8.0000];

and you want to integrate this from x = 0.25 to 1.75. We don't have data in those regions, so some interpolation is going to be needed. Here is the analytical integral and by numerical quadrature

i_analytical = 1/4*(1.75^4-0.25^4)
i = quad(f,0.25,1.75)
% they are practically the same.

i_analytical =

    2.3438


i =

    2.3437

One way to do this with the data provided is to use interpolation on a fine-spaced x-grid, and then use trapz on the resulting interpolated vectors.

xfine = linspace(0.25,1.75);
yinterp = interp1(x,y,xfine);
i4 = trapz(xfine,yinterp)
error = (i4 - i_analytical)/i_analytical

i4 =

    2.5315


error =

    0.0801

Another approach is to create a function handle to do the interpolation for you. This combines numerical data with the quad function!

finterp = @(X) interp1(x,y,X);
i5 = quad(finterp,0.25,1.75)
error = (i5 - i_analytical)/i_analytical

i5 =

    2.5312


error =

    0.0800

these two approaches are actually identical, as they are both based on linear interpolation. The second approach is slightly more compact and easier to evaluate multiple integrals. Compare:

i6 = quad(finterp,0.28,1.64)

i6 =

    1.9596

to:

xfine = linspace(0.28,1.64);
yinterp = interp1(x,y,xfine);
i7 = trapz(xfine,yinterp)
% One line of code vs. three.

i7 =

    1.9597

Summary

trapz and quad are functions for getting integrals. Both can be used with numerical data if interpolation is used.

Finally, see this post for an example of solving an integral equation using quad and fsolve.

% categories: basic matlab
% tags: integration

Published with MATLAB® 7.10