ODEs with discontinuous forcing functions

September 01, 2011 at 01:56 PM | categories: odes | View Comments

ODEs with discontinuous forcing functions

John Kitchin

Problem statement
Solution

Problem statement

Adapted from http://archives.math.utk.edu/ICTCM/VOL18/S046/paper.pdf A mixing tank initially contains 300 g of salt mixed into 1000 L of water. at t=0 min, a solution of 4 g/L salt enters the tank at 6 L/min. at t=10 min, the solution is changed to 2 g/L salt, still entering at 6 L/min. The tank is well stirred, and the tank solution leaves at a rate of 6 L/min. Plot the concentration of salt (g/L) in the tank as a function of time.

Solution

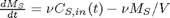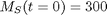A mass balance on the salt in the tank leads to this differential equation: $\frac{dM_S}{dt} = \nu C_{S,in}(t) - \nu M_S/V$ with the initial condition that $M_S(t=0)=300$

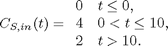
. The wrinkle is that $C_{S,in}(t) = \begin{array}{ll}�0 & t \le 0, \\�4 & 0 < t \le 10, \\�2 & t > 10. \end{array}$

function main

tspan = [0,15]; % min
Mo = 300; % gm salt
[t,M] = ode45(@mass_balance,tspan,Mo);

V = 1000; % L
plot(t,M/V,'b.-')
xlabel('Time (min)')
ylabel('Salt concentration (g/L)')

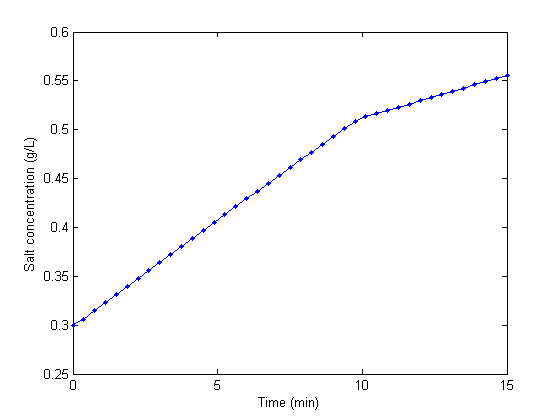You can see the discontinuity in the salt concentration at 10 minutes due to the discontinous change in the entering salt concentration.

'done'

ans =

done

discontinuous feed concentration function

function Cs = Cs_in(t)

if t < 0
    Cs = 0; % g/L
elseif t > 0 && t <= 10
    Cs = 4; % g/L
else
    Cs = 2; % g/L
end

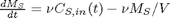
$\frac{dM_S}{dt} = \nu C_{S,in}(t) - \nu M_S/V$

function dMsdt = mass_balance(t,Ms)

V = 1000; % L
nu = 6;   % L/min
dMsdt = nu*Cs_in(t) - nu*Ms/V;

% categories: ODEs

Matlab in Chemical Engineering at CMU