Numerical solution to a simple ode:

Integrate this ordinary differential equation (ode)

Contents

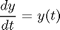
over the time span of 0 to 2. The initial condition is y(0) = 1.

to solve this equation, you need to create a function or function handle of the form: dydt = f(t,y) and then use one of the odesolvers, e.g. ode45.

function main

problem setup

y0 = 1; % initial condition y(t=t0)
t0 = 0; tend=2;
tspan = [t0 tend]; % span from t=0 to t=2
[t,y] = ode45(@myode,tspan,y0); % here is where you get the solution

plot(t,y)
xlabel('time')
ylabel('y(t)')

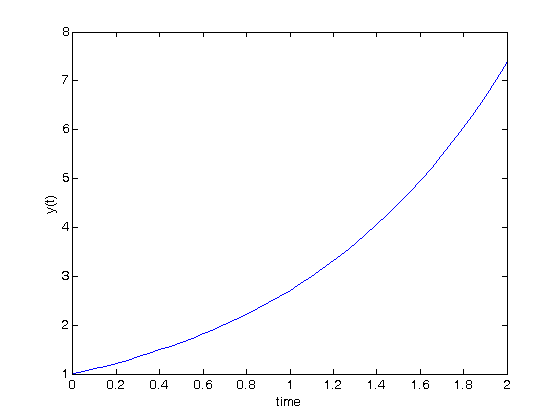
analytical solution

Hopefully you recognize the solution to this equation is 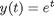. Let's plot that on the same graph. We will use a dashed red line

hold on
plot(t,exp(t),'r--')
legend('numerical solution','analytical solution')
% these are clearly the same solution.

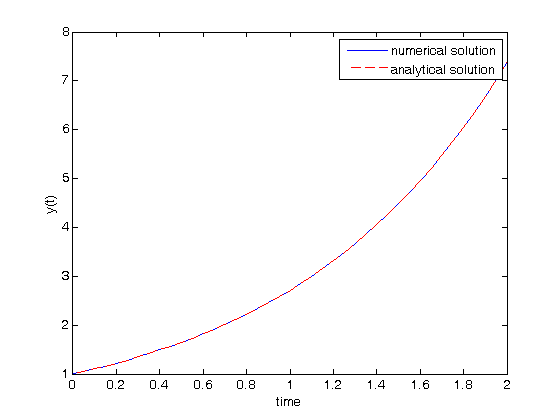
'end'

ans =

end

function dydt = myode(t,y)

differential equation to solve

dydt = y;

% categories: ODEs
% tags: math

Published with MATLAB® 7.10