Matlab in Chemical Engineering at CMU

Contents

Solving linear equations

Given these equations, find [x1; x2; x3].

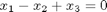
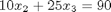
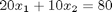
reference: Kreysig, Advanced Engineering Mathematics, 9th ed. Sec. 7.3

When solving linear equations, it is convenient to express the equations in matrix form:

A = [[1 -1 1];
    [0 10 25];
    [20 10 0]]

b = [0; 90; 80]  % b is a column vector

A =

     1    -1     1
     0    10    25
    20    10     0


b =

     0
    90
    80

making the augmented matrix

Awiggle = [A b]

Awiggle =

     1    -1     1     0
     0    10    25    90
    20    10     0    80

get the reduced row echelon form

rref(Awiggle)

ans =

     1     0     0     2
     0     1     0     4
     0     0     1     2

by inspection the solution is:

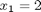
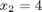
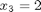
Let's test that out.

testing the solution

x = [2;4;2]
A*x
b
% you can see that A*x = b

x =

     2
     4
     2


ans =

     0
    90
    80


b =

     0
    90
    80

The shortcut way to solve this problem in Matlab with notation.

the backslash operator solves the equation Ax=b. Note that when there are more equations than unknowns

x = A\b

x =

    2.0000
    4.0000
    2.0000

linsolve function

x = linsolve(A,b)

x =

    2.0000
    4.0000
    2.0000

Not recommended solution methods

You may recall that a solution to

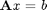
is:

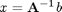
x = inv(A)*b

% while mathematically correct, computing the inverse of a matrix is
% computationally inefficient, and not recommended most of the time.

x =

    2.0000
    4.0000
    2.0000

What if no solution exists?

The following equations have no solution:

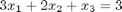
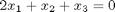
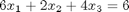
A = [[3 2 1];
    [2 1 1];
    [6 2 4]]

b = [3; 0; 6]

A =

     3     2     1
     2     1     1
     6     2     4


b =

     3
     0
     6

how do you know no solution exists?

rref([A b])
% the last line of this matrix states that 0 = 1. That is not true, which
% means there is no solution.

ans =

     1     0     1     0
     0     1    -1     0
     0     0     0     1

Matlab gives you a solution anyway! and a warning.

x = A\b


% categories: Linear algebra

Warning: Matrix is close to singular or badly scaled.
         Results may be inaccurate. RCOND = 3.364312e-018. 

x =

  1.0e+016 *

    1.8014
   -1.8014
   -1.8014

Published with MATLAB® 7.10