Matlab in Chemical Engineering at CMU

Contents

polynomials in matlab

polynomials can be represented as a vector of coefficients
4*x^3 + 3*x^2 -2*x + 10 = 0
can be represented as [4 3 -2 10]

ppar = [4 3 -2 10];

% we can evaluate the polynomial with the polyval command, e.g. to evaluate
% at x=3
polyval(ppar, 3)

ans =

   139

compare to

x=3;
4*x^3 + 3*x^2 -2*x + 10
% they are the same

ans =

   139

polynomial manipulations

matlab makes it easy to get the derivative and integral of a polynomial.

Consider:

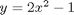
ppar = [2 0 -1];

polynomial derivatives

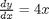
dpar = polyder(ppar)
% evaluate the derivative at x = 2
polyval(dpar,2)

dpar =

     4     0


ans =

     8

polynomial integrals

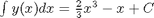
We assume .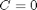

ipar = polyint(ppar)
% note that the integration constant is assumed to be zero. If it is not
% zero, use POLYINT(P,K) where K is the constant of integration.
%
% Compute the integral of the polynomial from 2 to 4
polyval(ipar,4) - polyval(ipar,2)
% analytically:
2/3*(4^3 - 2^3) + (-4 - (-2))

ipar =

    0.6667         0   -1.0000         0


ans =

   35.3333


ans =

   35.3333

getting the roots of a polynomial

roots are the x-values that make the polynomial equal to zero.

roots(ppar)

% the analytical solutions are +- sqrt(1/2)

% note that imaginary roots exist, e.g. x^2 + 1 = 0 has two roots, +-i
ppar = [1 0 1]
roots(ppar)

ans =

    0.7071
   -0.7071


ppar =

     1     0     1


ans =

        0 + 1.0000i
        0 - 1.0000i

application in thermodynamics

we need to find the volume that solves the van der waal equation:

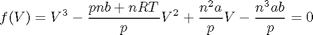
where a and b are constants.

% numerical values of the constants
a = 3.49e4;
b = 1.45;
p = 679.7;
T = 683;
n = 1.136;
R = 10.73;

% The van der waal equation is a polynomial
%  V^3 - (p*n*b+n*R*T)/p*V^2 + n^2*a/p*V - n^3*a*b/p = 0

%use commas for clarity in separation of terms
ppar = [1, -(p*n*b+n*R*T)/p, n^2*a/p,  -n^3*a*b/p];
roots(ppar)

% note that only one root is real. In this case that means there is only
% one phase present.

% categories: Basic matlab
% tags: math, thermodynamics

ans =

   5.0943          
   4.4007 + 1.4350i
   4.4007 - 1.4350i

Published with MATLAB® 7.10