Know your tolerance

Given:

Contents

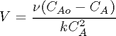
with the information given below, solve for the exit concentration. This should be simple. We use the units package to make sure we don't miss any units.

clear all; close all; clc
u = cmu.units;

Cao = 2*u.mol/u.L;
V = 10*u.L;
nu = 0.5*u.L/u.s;
k = 0.23 * u.L/u.mol/u.s;

function we need to solve

f = @(Ca) V - nu*(Cao - Ca)./(k*Ca.^2);

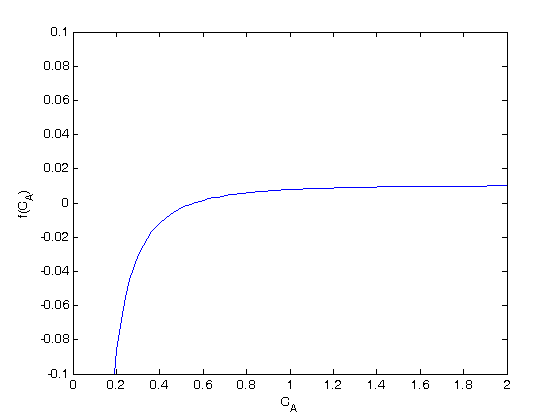
plot the function to estimate the solution

c = linspace(0,2)*u.mol/u.L;
plot(c/(u.mol/u.L),f(c))
ylim([-0.1 0.1]) % limit the y-range to see the zero easier
xlabel('C_A')
ylabel('f(C_A)')
% we want the value of C_A that makes f(C_A)=0. this happens around C_A=0.5

cguess = 0.5*u.mol/u.L;
c = fsolve(f,cguess)
% it is a little weird that the solution is the same as our initial guess.
% Usually the answer is at least a little different!

Equation solved at initial point.

fsolve completed because the vector of function values at the initial point
is near zero as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

  500.0000


Equation solved at initial point.

fsolve completed because the vector of function values at the initial point
is near zero as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.



500/m^3*mol

check your solution

z = f(c)
z.as(u.L)
% this is not really that close to zero, especially when you look at the
% units in L!

-0.00304348*m^3

ans =

-3.043*L

closer look at fsolve

Let's output some more information.

options = optimset('Display','iter');
[X,FVAL,EXITFLAG,OUTPUT] = fsolve(f,cguess,options)
% It should be a warning that zero iterations were taken! Our guess was
% probably not that good! The EXITFLAG=1 means the function ended ok as far
% as fsolve is concerned.

                                         Norm of      First-order   Trust-region
 Iteration  Func-count     f(x)          step         optimality    radius
     0          2    9.26276e-006                     1.85e-007               1

Equation solved at initial point.

fsolve completed because the vector of function values at the initial point
is near zero as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

  500.0000


                                         Norm of      First-order   Trust-region
 Iteration  Func-count     f(x)          step         optimality    radius
     0          2    9.26276e-006                     1.85e-007               1

Equation solved at initial point.

fsolve completed because the vector of function values at the initial point
is near zero as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.



500/m^3*mol
-0.00304348*m^3

EXITFLAG =

     1


OUTPUT = 

       iterations: 0
        funcCount: 2
        algorithm: 'trust-region dogleg'
    firstorderopt: 1.8526e-007
          message: [1x756 char]

The problem is bad scaling because the underlying units are stored in m^3, which results in very small numbers that are close to zero. So, fsolve sees a number it thinks is close to zero, and stops. One way to fix this is to decrease the tolerance on what constitutes zero.

options = optimset('TolFun',1e-9);
cguess = 0.5*u.mol/u.L;
[c2,FVAL,EXITFLAG,OUTPUT] = fsolve(f,cguess,options)
z2 = f(c2)
z2.as(u.L) % much closer to zero.

sprintf('The exit concentration is %1.2f mol/L', c2/(u.mol/u.L))

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the selected value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

  559.5545


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the selected value of the function tolerance, and
the problem appears regular as measured by the gradient.



559.554/m^3*mol
-1.24874e-006*m^3

EXITFLAG =

     1


OUTPUT = 

       iterations: 6
        funcCount: 14
        algorithm: 'trust-region dogleg'
    firstorderopt: 5.3309e-011
          message: [1x698 char]

-1.24874e-006*m^3

ans =

-0.001*L


ans =

The exit concentration is 0.56 mol/L

Rescaling the units

We can make the default length unit be dm, then the default volume unit will be 1L (dm^3). This will effectively rescale the function so that the default tolerance will be effective. Note you have to specify the unit for each unit in the order (length, time, mass, temperature, charge, mol).

u = cmu.unit.units('dm','s','kg','K','coul','mol');
Cao = 2*u.mol/u.L;
V = 10*u.L;
nu = 0.5*u.L/u.s;
k = 0.23 * u.L/u.mol/u.s;

% function we need to solve
f = @(Ca) V - nu*(Cao - Ca)./(k*Ca.^2);
cguess = 0.5*u.mol/u.L;
[c3,FVAL,EXITFLAG,OUTPUT] = fsolve(f,cguess)
sprintf('The exit concentration is %1.2f', c3)
% we were able to solve this more reasonably scaled problem without
% changing any default tolerances.

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




ans =

    0.5596


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.



0.559584/dm^3*mol
-3.9293e-012*dm^3

EXITFLAG =

     1


OUTPUT = 

       iterations: 4
        funcCount: 10
        algorithm: 'trust-region dogleg'
    firstorderopt: 1.6772e-010
          message: [1x695 char]


ans =

The exit concentration is 0.56 (dm^3*mol)^-1

'done'
% categories: nonlinear algebra
% tags: reaction engineering, units

ans =

done

Published with MATLAB® 7.10

Contents

Using cmu.units in Matlab for basic calculations

note you need to install the +cmu package for this to work.

clear all; clc; close all;

Load the units package

units is a new type of object in Matlab that stores the units, enforces proper unit algebra and works with most mathematical operations in Matlab. You load the units package into a variable; by convention: u the default set of base units are the SI units.

u = cmu.units;

Simple unit algebra

the basics of unit algebra are that like units can be added and subtracted. Unlike units can be multiplied and divided. when you assign a unit to a number, it is automatically converted into the base units.

5*u.kg % a mass
5*u.lb % another mass
6*u.m/u.s  % a velocity

1*u.m + 10*u.cm % this is ok, 1.1 m
% 1*u.m + 1*u.s  % this is not ok

5*kg
2.26796*kg
6*m/s
1.1*m

Temperature is a little special

most unit conversions are simple multiplications. Temperature conversions involve multiplication and an offset; e.g. F = C*9/5 + 32;

T = 298*u.K    % Kelvin is an absolute scale
Tf = 400*u.R   % Rankine is an absolute scale
T1 = u.degC(100) % this is 100 degC, and T1 is in Kelvin
T2 = u.degF(212) % this is 212 degF, and T2 is in Kelvin

% convert 32 degF to degC
u.degF2C(32)  %no units on the output
u.degC2F(100) %no units on the output

298*K
222.222*K
373.15*K
373.15*K

ans =

     0


ans =

   212

displaying units

a unit object has an "as" function that can display the unit in various forms

a = 1*u.kg;
a.as(u.lb)

% to do an actual conversion, you divide the unit by the units you want to
% convert to.
sprintf('%1.2f = %1.2f lb',a,a/u.lb)

ans =

2.205*lb


ans =

1.00 kg = 2.20 lb

Load the cmu.constants package

The gas constant, speed of light, etc... are stored in this package

clear all; u = cmu.units;
c = cmu.constants;
c.R  %the gas constant%% variations of the gas constant
c.R.as(u.J/u.mol/u.K)
c.R.as(u.J/(u.mol*u.K))
c.R.as(u.cal/u.mol/u.K)
c.R.as(u.dm^3*u.atm/u.mol/u.K)
c.R.as(u.BTU/u.lbmol/u.R)
c.R.as(u.ft^3*u.atm/(u.lbmol*u.R))

8.31447*m^2/s^2*kg/K/mol

ans =

8.314*J/mol/K


ans =

8.314*J/(mol*K)


ans =

1.986*cal/mol/K


ans =

0.082*dm^3*atm/mol/K


ans =

1.986*BTU/lbmol/R


ans =

0.730*ft^3*atm/(lbmol*R)

Arrays of units

t = [0 1 2 3 4]*u.s;
C = [5 3 1 0.5 0.05]*u.mol/u.L; % note these concentrations are stored
                                % internally as mol/m^3 because those are
                                % the base SI units

% we can change the units in a plot by converting them to the units we want
plot(t/u.min,C/(u.mol/u.L))
xlabel('Time (min)')
ylabel('Concentration (mol/L)')

units with Matlab functions

Many functions in Matlab such as ode45, ode15s, fzero, fsolve, min, max, etc... work with units. This works because we have overloaded these functions to work with units. Not all functions are overloaded though, so be careful! If you find you have lost the units, it means you used a function that was not overloaded. Please let us know about it!

functions that do not work with units

functions that require dimensionless arguments (e.g. trig functions, exp, log, etc...) will usually fail if you pass a unit in. You must divide the arguments by the appropriate units to make them dimensionless

a = 5*u.mol;
sin(a/u.mol)

ans =

   -0.9589

Alternative base units

you can specify 'SI', 'CGS' or 'American' as the base units SI/MKS: {'m','s','kg', 'K', 'mol','coul'} CGS: {'cm','s','gm','K', 'mol','coul'} American: {'in','s','lb','R', 'mol','coul'

u = cmu.units('American');
a = 2*u.ft
a.as(u.m)

% you can also specify which units are your base. Note the order of base
% units must be: length, time, mass, temperature, charge, mol
% and all of them must be specified.
u = cmu.unit.units('mm','min','ton','R','coul','mol');
a = u.cm
a.as(u.m)

24*in

ans =

0.610*m

10*mm

ans =

0.010*m

simplified units

there may be times when you need units conversion, but you only want simple numbers and not unit objects, e.g. because some Matlab function doesn't handle units. You can load the simple_units structure to get a set of conversion factors. Unit algebra is not used and units are kept track of, so you have to know what the units are.

u = cmu.unit.simple_units;
a = 1*u.kg
a/u.lb
a/u.min

% tags: units, +cmu

a =

    0.0011


ans =

    2.2046


ans =

    0.0011

Published with MATLAB® 7.10