A novel way to numerically estimate the derivative of a function - complex-step derivative approximation
December 25, 2011 at 12:28 AM | categories: miscellaneous | View Comments
A novel way to numerically estimate the derivative of a function - complex-step derivative approximation
John Kitchin
Adapted from http://biomedicalcomputationreview.org/2/3/8.pdf and http://dl.acm.org/citation.cfm?id=838250.838251
This posts introduces a novel way to numerically estimate the derivative of a function that does not involve finite difference schemes. Finite difference schemes are approximations to derivatives that become more and more accurate as the step size goes to zero, except that as the step size approaches the limits of machine accuracy, new errors can appear in the approximated results. In the references above, a new way to compute the derivative is presented that does not rely on differences!
The new way is: 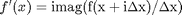 where the function
where the function 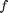 is evaluated in imaginary space with a small
is evaluated in imaginary space with a small 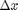 in the complex plane. The derivative is miraculously equal to the imaginary part of the result in the limit of
in the complex plane. The derivative is miraculously equal to the imaginary part of the result in the limit of  !
!
Contents
Example 1
This example comes from the first link. The derivative must be evaluated using the chain rule. We compare a forward difference, central difference and complex-step derivative approximations.
f = @(x) sin(3*x)*log(x);
ezplot(f)
format long
at x = 0.7
x = 0.7; h = 1e-7;
analytical derivative
dfdx_a = 3*cos(3*x)*log(x) + sin(3*x)/x
dfdx_a = 1.773354106237345
finite difference
dfdx_fd = (f(x) - f(x-h))/h
dfdx_fd = 1.773354270651062
central difference
dfdx_cd = (f(x+h)-f(x-h))/(2*h)
dfdx_cd = 1.773354105227831
complex method
dfdx_I = imag(f(x+h*i)/h)
dfdx_I = 1.773354106237384
compute errors
You can see the complex-step derivative approximation is several orders of magnitude more accurate than either of the finite difference methods.
dfdx_fd - dfdx_a dfdx_cd - dfdx_a dfdx_I - dfdx_a
ans =
1.644137173073546e-007
ans =
-1.009513361793779e-009
ans =
3.952393967665557e-014
another example
Let's use this method to verify the fundamental Theorem of Calculus, i.e. to evaluate the derivative of an integral function. Let 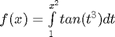 , and we now want to compute df/dx. Of course, this can be done analytically, but it is not trivial!
, and we now want to compute df/dx. Of course, this can be done analytically, but it is not trivial!
integrand = @(t) tan(t.^3); f = @(z) quad(integrand, 0,z.^2);
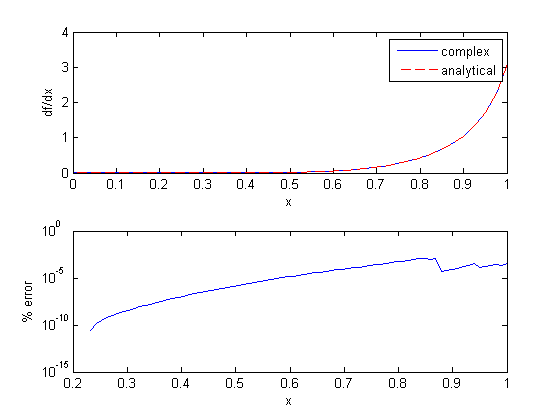
Lets evaluate the derivative over a range of x-values. The quad function is not vectorized for the limits, so we have to use arrayfun to map each x-value onto a vector of dfdx. The agreement here is very good, with the largest %%error being 0.0001%% near x=1. That interestingly does not get much better with smaller h.
x = linspace(0,1); dfdx = imag(arrayfun(f,(x+i*h))/h); dfdx_analytical = 2*x.*tan(x.^6); subplot(2,1,1) plot(x,dfdx,x,dfdx_analytical,'r--') xlabel('x') ylabel('df/dx') legend('complex','analytical') subplot(2,1,2) semilogy(x,(dfdx-dfdx_analytical)./dfdx_analytical*100) xlabel('x') ylabel('% error')
don't get too complacent though!
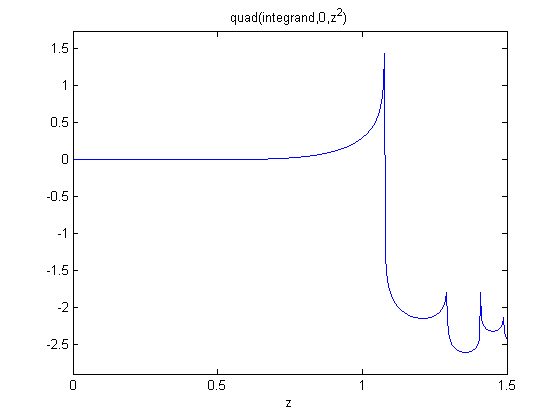
Here is an example that fails to agree!
x = linspace(0,1.5); dfdx = imag(arrayfun(f,(x+i*h))/h); dfdx_analytical = 2*x.*tan(x.^6); figure plot(x,dfdx,x,dfdx_analytical,'r--') legend('complex','analytical','location','best')
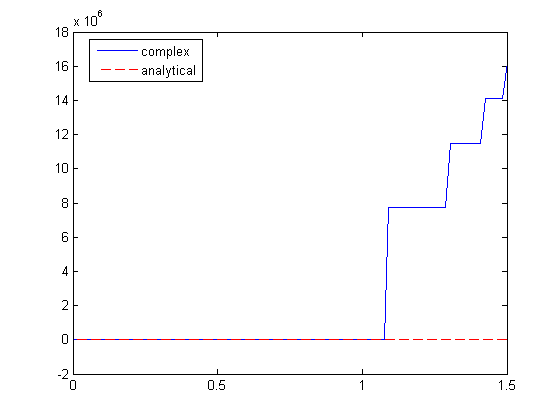
I guess the reason for the failure appears to be related to the singularity at x = 1.1. It is not clear why that causes the estimated derivative to blow up though, since it works everywhere else. It appears there is a step change at each singularity in the function.
ezplot(f,[0,1.5])
Summary
Using this simple formula 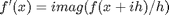 to approximate a derivative is one of the most interesting math facts I can't believe I didn't know before this post!
to approximate a derivative is one of the most interesting math facts I can't believe I didn't know before this post!
% categories: Miscellaneous
 in the temperature range of 500K to 1000K.
in the temperature range of 500K to 1000K. and
and 
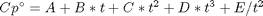
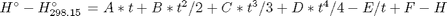
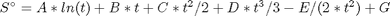
 , and
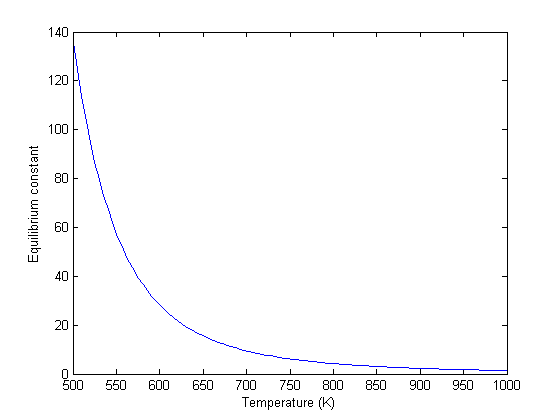
, and 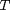 is the temperature in Kelvin. We can use this data to calculate equilibrium constants in the following manner. First, we have heats of formation at standard state for each compound; for elements, these are zero by definition, and for non-elements, they have values available from the NIST webbook. There are also values for the absolute entropy at standard state. Then, we have an expression for the change in enthalpy from standard state as defined above, as well as the absolute entropy. From these we can derive the reaction enthalpy, free energy and entropy at standard state, as well as at other temperatures.
is the temperature in Kelvin. We can use this data to calculate equilibrium constants in the following manner. First, we have heats of formation at standard state for each compound; for elements, these are zero by definition, and for non-elements, they have values available from the NIST webbook. There are also values for the absolute entropy at standard state. Then, we have an expression for the change in enthalpy from standard state as defined above, as well as the absolute entropy. From these we can derive the reaction enthalpy, free energy and entropy at standard state, as well as at other temperatures.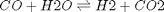 .
.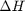 and
and 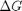
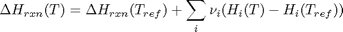
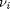 are the stoichiometric coefficients of each species, with appropriate sign for reactants and products, and
are the stoichiometric coefficients of each species, with appropriate sign for reactants and products, and 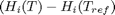 is precisely what is calculated for each species with the equations
is precisely what is calculated for each species with the equations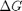 varies with temperature
varies with temperature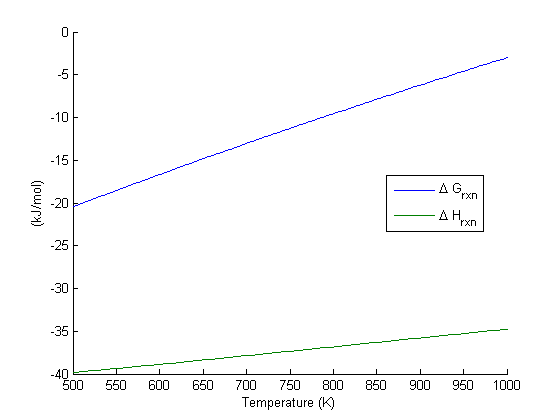
 be the extent of reaction, so that
be the extent of reaction, so that 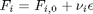 . For reactants,
. For reactants, 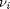 is negative, and for products,
is negative, and for products,